किसी वृत्त की परिधि की सही गणना कैसे करें?
वृत्त की परिधि एक बुनियादी और आवश्यक गणित ज्ञान है जिसे प्राथमिक या मध्य विद्यालय में पढ़ाया जाता है। वृत्त की परिधि में महारत हासिल करना उन छात्रों के लिए आवश्यक है जो हाई स्कूल और कॉलेज में अधिक उन्नत गणित पाठ्यक्रम करने की योजना बनाते हैं और SAT और ACT जैसी मानकीकृत परीक्षाओं की तैयारी करते हैं।
इस लेख में 10 वृत्त की परिधि प्रश्नोत्तरी एक वृत्त की त्रिज्या, व्यास और परिधि ज्ञात करने की आपकी समझ का परीक्षण करने के लिए डिज़ाइन की गई है।
सामग्री की तालिका:
वृत्त की परिधि का सूत्र
परीक्षा देने से पहले, आइए कुछ महत्वपूर्ण जानकारी पुनः याद कर लें!
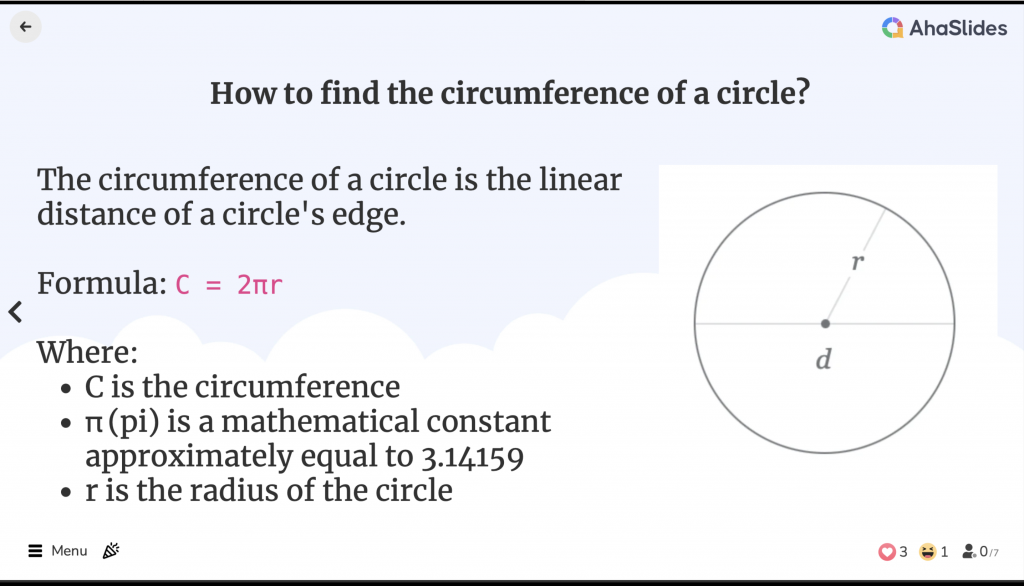
एक वृत्त की परिधि कितनी होती है?
किसी वृत्त की परिधि, वृत्त के किनारे की रैखिक दूरी होती है। यह ज्यामितीय आकार की परिधि के बराबर होती है, हालाँकि परिधि शब्द का इस्तेमाल सिर्फ़ बहुभुजों के लिए किया जाता है।
किसी वृत्त की परिधि कैसे ज्ञात करें?
वृत्त की परिधि का सूत्र है:
C = 2πr
जहाँ:
- C परिधि है
- π (पाई) एक गणितीय स्थिरांक है जो लगभग 3.14159 के बराबर है
- r वृत्त की त्रिज्या है
त्रिज्या वृत्त के केंद्र से किनारे पर स्थित किसी भी बिंदु तक की दूरी है।
व्यास त्रिज्या का दोगुना है, इसलिए परिधि को इस प्रकार भी व्यक्त किया जा सकता है:
C = πd
जहाँ:
- d व्यास है
उदाहरण के लिए, यदि किसी वृत्त की त्रिज्या 5 सेमी है, तो परिधि होगी:
C = 2πr = 2π * 5 cm = 10π cm
≈ 31.4 सेमी (2 दशमलव स्थानों तक पूर्णांकित)
AhaSlides से अधिक सुझाव
- कक्षा में मज़ा अभ्यास के लिए 70+ गणित प्रश्नोत्तरी प्रश्न
- ऊब गए K10 छात्रों के लिए 12 सर्वश्रेष्ठ कक्षा गणित खेल
- वयस्कों के लिए ब्रेन टीज़र पर 60 अद्भुत विचार | 2023 अपडेट
AhaSlides सर्वश्रेष्ठ क्विज़ निर्माता है
बोरियत दूर करने के लिए हमारी व्यापक टेम्पलेट लाइब्रेरी के साथ तुरंत इंटरैक्टिव गेम बनाएं

वृत्त की परिधि प्रश्नोत्तरी
प्रश्न 1: यदि एक वृत्ताकार स्विमिंग पूल की परिधि 50 मीटर है, तो इसकी त्रिज्या क्या है?
ए. 7.95 मीटर
बी. 8.00 मीटर
सी. 15.91 मीटर
डी. 25 मीटर
✅ सही जवाब:
ए. 7.95 मीटर
स्पष्टीकरण:
सूत्र C = 2πr को पुनर्व्यवस्थित करके तथा r के लिए हल करके त्रिज्या ज्ञात की जा सकती है: r = C / (2π)। 50 मीटर की दी गई परिधि को जोड़कर तथा π को 3.14 के बराबर मानकर, हम पाते हैं कि त्रिज्या लगभग 7.95 मीटर है।
प्रश्न 2: एक वृत्त का व्यास 14 इंच है। इसकी त्रिज्या क्या है?
उ. 28 इंच
बी.14 इंच
सी. 21 इंच
डी. 7 इंच
✅ सही जवाब:
डी. 7 इंच
स्पष्टीकरण:
चूंकि व्यास त्रिज्या की लंबाई का दोगुना है (d = 2r), आप व्यास को 2 से विभाजित करके त्रिज्या ज्ञात कर सकते हैं (r = d / 2)। इस स्थिति में, दिए गए 14 इंच के व्यास को 2 से विभाजित करने पर 7 इंच की त्रिज्या प्राप्त होती है।

प्रश्न 3: वृत्त के व्यास और परिधि के बीच संबंध के बारे में निम्नलिखित में से कौन सा कथन सत्य है?
A. व्यास परिधि का आधा है।
B. व्यास परिधि के समान है।
C. व्यास परिधि का दोगुना है।
D. व्यास परिधि का π गुना है।
✅ सही जवाब:
A. व्यास परिधि का आधा है।
स्पष्टीकरण:
व्यास त्रिज्या के 2 गुना के बराबर है, जबकि परिधि त्रिज्या के 2π गुना के बराबर है। इसलिए, व्यास परिधि का आधा है।
प्रश्न 4: जिस मेज़ पर हमें बैठना है उसकी परिधि 6.28 गज है। हमें मेज़ का व्यास ज्ञात करना है।
ए. 1 यार्ड
बी. 2 गज
सी. 3 गज
डी. 4 गज
✅ सही जवाब:
बी. 2 गज
स्पष्टीकरण:
किसी वृत्त की परिधि की गणना व्यास को पाई (π) से गुणा करके की जाती है। इस मामले में, परिधि 6.28 गज दी गई है। व्यास ज्ञात करने के लिए, हमें परिधि को पाई से विभाजित करना होगा। 6.28 गज को पाई से विभाजित करने पर हमें लगभग 2 गज प्राप्त होता है। इसलिए, मेज का व्यास 2 गज है।
प्रश्न 5: एक वृत्ताकार बगीचे की परिधि 36 मीटर है। बगीचे की अनुमानित त्रिज्या क्या है?
ए. 3.14 मीटर
बी. 6 मीटर
सी. 9 मीटर
डी. 18 मीटर
✅ सही जवाब:
सी. 9 मीटर
स्पष्टीकरण:
त्रिज्या ज्ञात करने के लिए परिधि के सूत्र का उपयोग करें: C = 2πr. त्रिज्या ज्ञात करने के लिए सूत्र को पुनः व्यवस्थित करें: r = C / (2π). 36 मीटर की दी गई परिधि को जोड़ने और π के अनुमानित मान को 3.14 के रूप में उपयोग करने पर, आपको r = 36 / (2 * 3.14) ≈ 9 मीटर मिलता है।
प्रश्न 6: एक वृत्ताकार स्विमिंग पूल की त्रिज्या 8 मीटर है। एक चक्कर पूरा करने में एक तैराक पूल के चारों ओर लगभग कितनी दूरी तय करता है?
ए. 16 मीटर
बी. 25 मीटर
सी. 50 मीटर
डी. 100 मीटर
✅ सही जवाब:
सी. 50 मीटर
स्पष्टीकरण:
एक चक्कर में तैराक द्वारा पूल के चारों ओर तय की गई दूरी का पता लगाने के लिए, आप परिधि सूत्र (C = 2πr) का उपयोग करते हैं। इस मामले में, यह 2 * 3.14 * 8 मीटर ≈ 50.24 मीटर है, जो लगभग 50 मीटर है।
प्रश्न 7: कक्षा में हुला हूप को मापते समय, समूह C ने पाया कि इसकी त्रिज्या 7 इंच थी। हुला हूप की परिधि क्या है?
उ. 39.6 इंच
बी. 37.6 इंच
सी. 47.6 इंच
डी. 49.6 इंच
✅ सही जवाब:
सी. 47.6 इंच
स्पष्टीकरण:
किसी वृत्त की परिधि सूत्र C = 2πr का उपयोग करके ज्ञात की जा सकती है, जहाँ r वृत्त की त्रिज्या है। इस मामले में, हुला हूप की त्रिज्या 7 इंच दी गई है। इस मान को सूत्र में डालने पर, हमें C = 2π(7) = 14π इंच मिलता है। π को 3.14 के लगभग मान पर, हम परिधि की गणना 14(3.14) = 43.96 इंच के रूप में कर सकते हैं। निकटतम दसवें तक पूर्णांकित करने पर, परिधि 47.6 इंच है, जो दिए गए उत्तर से मेल खाती है।
प्रश्न 8: एक अर्धवृत्त की त्रिज्या 10 मीटर है। इसका परिमाप क्या है?
ए. 20 मीटर
बी. 15 मीटर
सी. 31.42 मीटर
डी. 62.84 मीटर
✅ सही जवाब:
सी. 31.42 मीटर
स्पष्टीकरण: अर्धवृत्त का परिमाप ज्ञात करने के लिए 10 मीटर त्रिज्या वाले पूर्ण वृत्त की आधी परिधि की गणना करें।

प्रश्न 9: बास्केटबॉल टीम 5.6 इंच त्रिज्या वाली गेंद से खेलती है। प्रत्येक बास्केटबॉल की परिधि कितनी है?
उ. 11.2 इंच
बी. 17.6 इंच
सी. 22.4 इंच
डी. 35.2 इंच
✅ सही जवाब:
सी. 22.4 इंच
व्याख्या:
आप वृत्त की परिधि के लिए सूत्र का उपयोग कर सकते हैं, जो C = 2πr है। दी गई त्रिज्या 5.6 इंच है। इस मान को सूत्र में डालें, हमारे पास C = 2π * 5.6 इंच है। C ≈ 2 * 3.14 * 5.6 इंच। C ≈ 11.2 * 5.6 इंच। C ≈ 22.4 इंच। तो, प्रत्येक बास्केटबॉल की परिधि लगभग 22.4 इंच है। यह बास्केटबॉल के चारों ओर की दूरी को दर्शाता है।
प्रश्न 10: सारा और उसकी दो सहेलियाँ अपनी सभा के लिए एक गोलाकार पिकनिक टेबल बना रही थीं। उन्हें पता था कि सभी के टेबल के चारों ओर आराम से बैठने के लिए, उन्हें 18 फ़ीट की परिधि की आवश्यकता होगी। सही परिधि प्राप्त करने के लिए पिकनिक टेबल का व्यास कितना होना चाहिए?
उ. 3 फीट
बी. 6 फीट
सी. 9 फीट
डी. 12 फीट
✅ सही जवाब:
बी. 6 फीट
स्पष्टीकरण:
त्रिज्या ज्ञात करने के लिए परिधि को 2π से विभाजित करें, हमारे पास है r = C / (2π) r = 18 फीट / (2 * 3.14) r ≈ 18 फीट / 6.28 r ≈ 2.87 फीट (निकटतम सौवें तक पूर्णांकित)।
अब, व्यास ज्ञात करने के लिए, बस त्रिज्या को दोगुना करें: व्यास = 2 * त्रिज्या व्यास ≈ 2 * 2.87 फीट व्यास ≈ 5.74 फीट। तो, पिकनिक टेबल का व्यास लगभग 5.74 फीट होना चाहिए
चाबी छीन लेना
अहास्लाइड्स यह सबसे अच्छा इंटरैक्टिव क्विज़ मेकर है जिसका उपयोग शिक्षा, प्रशिक्षण या मनोरंजन के उद्देश्यों के लिए किया जा सकता है। AhaSlides पर तुरंत जाकर मुफ़्त क्विज़ पाएँ अनुकूलन योग्य टेम्पलेट और उन्नत सुविधाएँ!
अक्सर पूछे जाने वाले प्रश्न
एक वृत्त का 2πr क्या है?
2πr वृत्त की परिधि का सूत्र है। इस सूत्र में:
- "2" दर्शाता है कि आप त्रिज्या की दुगुनी लंबाई ले रहे हैं। परिधि वृत्त के चारों ओर की दूरी है, इसलिए आपको वृत्त के चारों ओर एक बार और फिर से जाना होगा, यही कारण है कि हम 2 से गुणा करते हैं।
- "π" (पाई) एक गणितीय स्थिरांक है जो लगभग 3.14159 के बराबर है। इसका उपयोग इसलिए किया जाता है क्योंकि यह वृत्त की परिधि और व्यास के बीच के संबंध को दर्शाता है।
- “r” वृत्त की त्रिज्या को दर्शाता है, जो वृत्त के केंद्र से उसकी परिधि पर स्थित किसी भी बिंदु की दूरी है।
परिधि 2πr क्यों है?
The formula for the circumference of a circle, C = 2��r, comes from the definition of pi (π) and the geometric properties of a circle. Pi (π) represents the ratio of the circumference of a circle to its diameter. When you multiply the radius (r) by 2π, you essentially calculate the distance around the circle, which is the definition of circumference.
क्या परिधि त्रिज्या की 3.14 गुना है?
नहीं, परिधि त्रिज्या के ठीक 3.14 गुना नहीं है। परिधि और वृत्त की त्रिज्या के बीच का संबंध सूत्र C = 2πr द्वारा दिया जाता है। जबकि π (पाई) लगभग 3.14159 है, परिधि त्रिज्या के 2 गुना π गुना है। इसलिए, परिधि त्रिज्या के 3.14 गुना से अधिक है; यह त्रिज्या के 2 गुना π गुना है।
रेफरी: ओमनी कैक्यूलेटर | प्रोप्रो