Ինչպե՞ս ճիշտ հաշվարկել շրջանագծի պարագիծը։
Շրջանակի շրջագիծը տարրական և պարտադիր մաթեմատիկական գիտելիք է, որը ներդրվում է տարրական կամ միջնակարգ դպրոցում: Շրջանակի շրջագիծը տիրապետելը կարևոր է այն աշակերտների համար, ովքեր պլանավորում են ավագ դպրոցում և քոլեջում անցնել ավելի խորացված մաթեմատիկայի դասընթացների և պատրաստվել ստանդարտացված քննությունների, ինչպիսիք են SAT-ը և ACT-ը:
Այս հոդվածում շրջանագծի 10-րդ չափի թեստը նախատեսված է շրջանագծի շառավղի, տրամագծի և շրջագծի չափման վերաբերյալ ձեր գիտելիքները ստուգելու համար։
Բովանդակություն:
Շրջանակի շրջագծի բանաձևը
Թեստը հանձնելուց առաջ, եկեք կրկնենք մի քանի կարևոր տեղեկություններ։
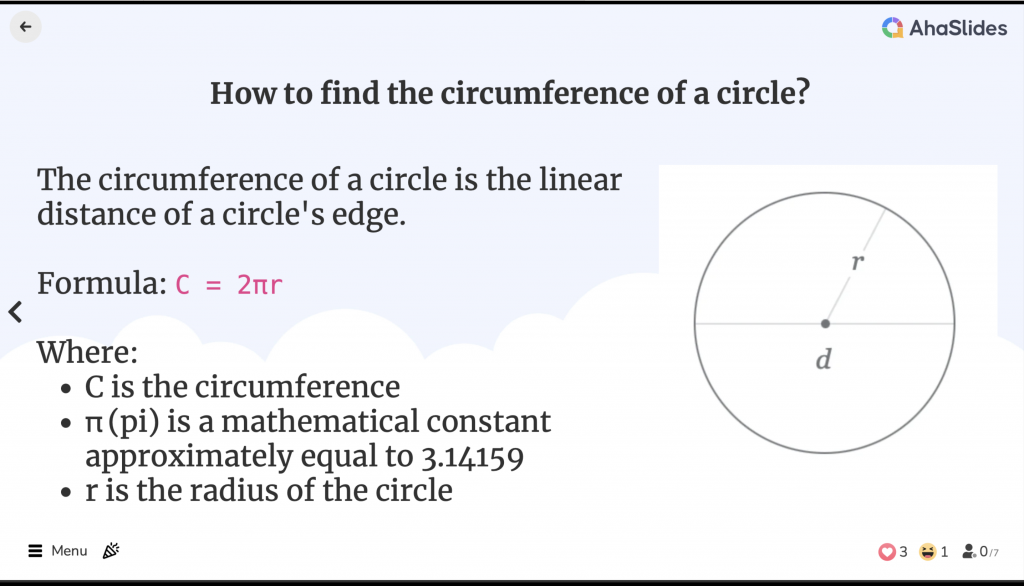
Որքա՞ն է շրջանագծի պարագիծը։
Շրջանակի շրջագիծը շրջանագծի եզրի գծային հեռավորությունն է։ Այն համարժեք է երկրաչափական պատկերի պարագծին, չնայած «պարագիծ» տերմինն օգտագործվում է միայն բազմանկյունների համար։
Ինչպե՞ս գտնել շրջանագծի պարագիծը։
Շրջանակի շրջագծի բանաձևը հետևյալն է.
C = 2πr
որտեղ
- C-ն շրջագիծն է
- π (pi)-ն մաթեմատիկական հաստատուն է, որը մոտավորապես հավասար է 3.14159-ի
- r-ը շրջանագծի շառավիղն է
Շառավիղը շրջանագծի կենտրոնից մինչև եզրի ցանկացած կետ ընկած հեռավորությունն է։
Տրամագիծը շառավղի կրկնակին է, ուստի շրջագիծը կարող է նաև արտահայտվել հետևյալ կերպ.
C = πd
որտեղ
- d-ն տրամագիծն է
Օրինակ, եթե շրջանագծի շառավիղը 5 սմ է, ապա շրջագիծը կլինի՝
C = 2πr = 2π * 5 cm = 10π cm
≈ 31.4 սմ (կլորացված մինչև 2 տասնորդական նիշ)
Ավելի շատ խորհուրդներ AhaSlides-ից
- 70+ մաթեմատիկական վիկտորինայի հարցեր դասարանում զվարճալի վարժությունների համար
- 10 Լավագույն դասարանային մաթեմատիկայի խաղեր Bored K12 ուսանողների համար
- 60 ապշեցուցիչ գաղափարներ մեծահասակների համար ուղեղային զնգոցների մասին | 2023 Թարմացումներ
AhaSlides-ը վիկտորինայի վերջնական ստեղծողն է
Մի ակնթարթում պատրաստեք ինտերակտիվ խաղեր մեր ընդարձակ կաղապարների գրադարանի միջոցով՝ ձանձրույթը վերացնելու համար

Շրջանակի շրջագիծ թեստ
Հարց 1. Եթե շրջանաձև լողավազանի շրջագիծը 50 մետր է, որքա՞ն է դրա շառավիղը։
Ա. 7.95 մետր
Բ. 8.00 մետր
Մոտ 15.91 մետր
Դ. 25 մետր
✅ Ճիշտ պատասխան:
Ա. 7.95 մետր
Բացատրությունը.
Շառավիղը կարելի է գտնել՝ վերադասավորելով C = 2πr բանաձևը և լուծելով r-ը՝ r = C / (2π): Հաշվարկելով տրված 50 մետր շրջագիծը և մոտավորապես π-ն հասցնելով 3.14-ի, ստանում ենք, որ շառավիղը մոտավորապես 7.95 մետր է:
Հարց 2. Շրջանակի տրամագիծը 14 դյույմ է։ Որքա՞ն է նրա շառավիղը։
A. 28 դյույմ
Բ. 14 դյույմ
C. 21 դյույմ
D. 7 դյույմ
✅ Ճիշտ պատասխան:
D. 7 դյույմ
Բացատրությունը.
Քանի որ տրամագիծը շառավղի երկարության կրկնակին է (d = 2r), շառավիղը կարող եք գտնել՝ տրամագիծը բաժանելով 2-ի (r = d / 2): Այս դեպքում, տրված 14 դյույմ տրամագիծը 2-ի բաժանելով, կստանաք 7 դյույմ շառավիղ:

Հարց 3։ Հետևյալ պնդումներից որն է ճիշտ շրջանագծի տրամագծի և պարագծի միջև եղած կապի վերաբերյալ։
Ա. Տրամագիծը շրջագծի կեսն է։
Բ. Տրամագիծը նույնն է, ինչ շրջագիծը։
Գ. Տրամագիծը կրկնակի մեծ է շրջագծից։
Դ. Տրամագիծը π բազմապատկած է շրջագծից։
✅ Ճիշտ պատասխան:
Ա. Տրամագիծը շրջագծի կեսն է։
Բացատրությունը.
Տրամագիծը հավասար է շառավղի 2-ապատիկին, մինչդեռ շրջագիծը հավասար է շառավղի 2π-ապատիկին։ Հետևաբար, տրամագիծը շրջագծի կեսն է։
Հարց 4. Սեղանի շրջագիծը, որի շուրջ մենք պետք է նստենք, 6.28 յարդ է։ Մենք պետք է գտնենք սեղանի տրամագիծը։
Ա. 1 յարդ
Բ. 2 յարդ
Գ. 3 յարդ
Դ. 4 յարդ
✅ Ճիշտ պատասխան:
Բ. 2 յարդ
Բացատրությունը.
Շրջանակի շրջագիծը հաշվարկվում է տրամագիծը π (π) թվով բազմապատկելով։ Այս դեպքում շրջագիծը տրվում է 6.28 յարդ։ Տրամագիծը գտնելու համար մենք պետք է շրջագիծը բաժանենք π թվի վրա։ 6.28 յարդը պի թվի վրա բաժանելիս կստանանք մոտավորապես 2 յարդ։ Հետևաբար, սեղանի տրամագիծը 2 յարդ է։
Հարց 5. Շրջանաձև այգին ունի 36 մետր շրջագիծ։ Որքա՞ն է այգու մոտավոր շառավիղը։
Ա. 3.14 մետր
Բ. 6 մետր
Մոտ 9 մետր
Դ. 18 մետր
✅ Ճիշտ պատասխան:
Մոտ 9 մետր
Բացատրությունը.
Շառավիղը գտնելու համար օգտագործեք շրջագծի բանաձևը՝ C = 2πr: Վերադասավորեք բանաձևը՝ շառավիղը գտնելու համար՝ r = C / (2π): Հաշվարկելով տրված 36 մետր շրջագիծը և π-ի մոտավոր արժեքը որպես 3.14 օգտագործելով՝ կստանաք r = 36 / (2 * 3.14) ≈ 9 մետր:
Հարց 6. Շրջանաձև լողավազանն ունի 8 մետր շառավղ։ Մոտավորապես որքա՞ն հեռավորություն է անցնում լողորդը լողավազանի շուրջը մեկ շրջան անցնելիս։
Ա. 16 մետր
Բ. 25 մետր
Մոտ 50 մետր
Դ. 100 մետր
✅ Ճիշտ պատասխան:
Մոտ 50 մետր
Բացատրությունը.
Լողորդի լողավազանի շուրջ մեկ շրջանի ընթացքում անցած հեռավորությունը գտնելու համար օգտագործվում է շրջագծի բանաձևը (C = 2πr): Այս դեպքում այն հավասար է 2 * 3.14 * 8 մետր ≈ 50.24 մետրի, որը մոտավորապես 50 մետր է:
Հարց 7. Դասարանում հուլա հուպը չափելիս C խումբը հայտնաբերեց, որ այն ունի 7 դյույմ շառավիղ։ Որքա՞ն է հուլա հուպի շրջագիծը։
A. 39.6 դյույմ
B. 37.6 դյույմ
C. 47.6 դյույմ
D. 49.6 դյույմ
✅ Ճիշտ պատասխան:
C. 47.6 դյույմ
Բացատրությունը.
Շրջանակի շրջագիծը կարելի է գտնել C = 2πr բանաձևով, որտեղ r-ը շրջանագծի շառավիղն է։ Այս դեպքում հուլա հուպի շառավիղը տրված է որպես 7 դյույմ։ Այս արժեքը բանաձևի մեջ տեղադրելով՝ ստանում ենք C = 2π(7) = 14π դյույմ։ Մոտավորելով π-ն 3.14-ի, կարող ենք շրջանագիծը հաշվարկել որպես 14(3.14) = 43.96 դյույմ։ Կլորացնելով մինչև մոտակա տասնորդականը, շրջանագիծը կազմում է 47.6 դյույմ, որը համապատասխանում է տրված պատասխանին։
Հարց 8. Կիսաշրջանի շառավիղը 10 մետր է։ Որքա՞ն է դրա պարագիծը։
Ա. 20 մետր
Բ. 15 մետր
Մոտ 31.42 մետր
Դ. 62.84 մետր
✅ Ճիշտ պատասխան:
Մոտ 31.42 մետր
Բացատրությունը. Կիսաշրջանի պարագիծը գտնելու համար հաշվարկեք 10 մետր շառավղով լրիվ շրջանագծի կեսը։

Հարց 9. Բասկետբոլի թիմը խաղում է 5.6 դյույմ շառավղով գնդակով։ Որքա՞ն է յուրաքանչյուր բասկետբոլի գնդակի շրջագիծը։
A. 11.2 դյույմ
B. 17.6 դյույմ
C. 22.4 դյույմ
D. 35.2 դյույմ
✅ Ճիշտ պատասխան:
C. 22.4 դյույմ
բացատրություն:
Կարող եք օգտագործել շրջանագծի շրջագծի բանաձևը, որը C = 2πr է: Տրված շառավիղը 5.6 դյույմ է: Մուտքագրեք այս արժեքը բանաձևի մեջ, մենք ունենք C = 2π * 5.6 դյույմ: C ≈ 2 * 3.14 * 5.6 դյույմ: C ≈ 11.2 * 5.6 դյույմ: C ≈ 22.4 դյույմ: Այսպիսով, յուրաքանչյուր բասկետբոլի գնդակի շրջագիծը մոտավորապես 22.4 դյույմ է: Սա ներկայացնում է բասկետբոլի գնդակի շուրջը եղած հեռավորությունը:
Հարց 10. Սառան և նրա երկու ընկերները շրջանաձև պիկնիկի սեղան էին պատրաստում իրենց հավաքույթի համար: Նրանք գիտեին, որ որպեսզի բոլորը հարմարավետ նստեն սեղանի շուրջ, իրենց անհրաժեշտ է 18 ոտնաչափ շրջագիծ: Ի՞նչ տրամագիծ պետք է ունենա պիկնիկի սեղանը՝ ճիշտ շրջագիծ ստանալու համար:
A. 3 ոտնաչափ
B. 6 ոտնաչափ
C. 9 ոտնաչափ
D. 12 ոտնաչափ
✅ Ճիշտ պատասխան:
B. 6 ոտնաչափ
Բացատրությունը.
Շառավիղը գտնելու համար շրջագիծը բաժանեք 2π-ի, կստանանք՝ r = C / (2π) r = 18 ոտնաչափ / (2 * 3.14) r ≈ 18 ոտնաչափ / 6.28 r ≈ 2.87 ոտնաչափ (կլորացված մինչև հարյուրերորդականը):
Հիմա, տրամագիծը գտնելու համար պարզապես կրկնապատկեք շառավիղը՝ Տրամագիծ = 2 * Շառավիղ Տրամագիծ ≈ 2 * 2.87 ոտնաչափ Տրամագիծ ≈ 5.74 ոտնաչափ։ Այսպիսով, պիկնիկի սեղանի տրամագիծը պետք է լինի մոտավորապես 5.74 ոտնաչափ։
Հիմնական ճարպերը
AhaSlides- ը լավագույն ինտերակտիվ վիկտորինաների ստեղծողն է, որը կարող է օգտագործվել կրթության, վերապատրաստման կամ զվարճանքի նպատակներով: Անմիջապես ստուգեք AhaSlides-ը՝ անվճար ստանալու համար: հարմարեցված կաղապարներ և առաջադեմ գործառույթներ!
Հաճախակի տրվող հարցեր
Որքա՞ն է շրջանագծի 2πr-ը։
2πr-ը շրջանագծի պարագծի բանաձևն է։ Այս բանաձևում՝
- «2»-ը նշանակում է, որ դուք վերցնում եք շառավղի կրկնակի երկարությունը։ Շրջագիծը շրջանագծի շուրջն անցած հեռավորությունն է, ուստի դուք պետք է շրջանագծի շուրջը պտտվեք մեկ անգամ, ապա կրկին, այդ պատճառով մենք բազմապատկում ենք 2-ով։
- «π»-ն (pi) մաթեմատիկական հաստատուն է, որը մոտավորապես հավասար է 3.14159-ի։ Այն օգտագործվում է, քանի որ ներկայացնում է շրջանագծի և տրամագծի միջև եղած կապը։
- «r»-ը ներկայացնում է շրջանագծի շառավիղը, որը շրջանագծի կենտրոնից մինչև նրա շրջագծի ցանկացած կետ եղած հեռավորությունն է։
Ինչո՞ւ է շրջագիծը 2πr։
Շրջանակի շրջագծի C = 2πr բանաձևը ծագում է π (π) թվի սահմանումից և շրջանագծի երկրաչափական հատկություններից: Պի (π)-ն ներկայացնում է շրջանագծի և դրա տրամագծի հարաբերությունը: Երբ շառավիղը (r) բազմապատկում եք 2π-ով, դուք, ըստ էության, հաշվարկում եք շրջանագծի շուրջ հեռավորությունը, որը շրջագծի սահմանումն է:
Շրջագիծը շառավիղից 3.14 անգամ մեծ է՞։
Ոչ, շրջագիծը ճիշտ շառավղի 3.14 անգամը չէ։ Շրջանակի և շառավղի միջև եղած կապը տրվում է C = 2πr բանաձևով։ Մինչդեռ π (π)-ն մոտավորապես 3.14159 է, շրջագիծը շառավղի 2 անգամը π-ն է։ Այսպիսով, շրջագիծը շառավղի 3.14 անգամից ավելին չէ. այն շառավղի 2 անգամը π-ն է։
Ref: Omni Caculator | պրոֆ