원의 둘레를 정확히 계산하는 방법은?
원의 둘레는 초등학교나 중학교에서 배우는 기본적이고 필수적인 수학 지식입니다. 고등학교와 대학교에서 더 심화된 수학 과정을 수강하고 SAT나 ACT와 같은 표준화된 시험을 준비하려는 학생들에게 원의 둘레를 완벽하게 이해하는 것은 필수적입니다.
이 기사의 원의 둘레 퀴즈는 원의 반지름, 지름, 둘레를 구하는 방법에 대한 이해도를 테스트하기 위해 고안되었습니다.
목차 :
원의 둘레 공식
시험을 보기 전에, 몇 가지 중요한 정보를 다시 한번 살펴보겠습니다!
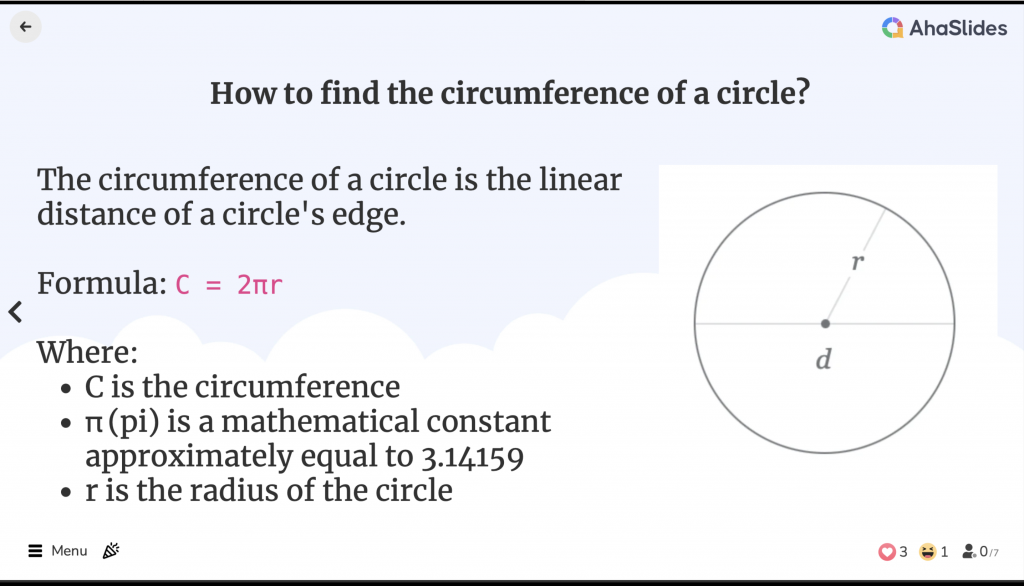
원의 둘레는 얼마입니까?
원의 둘레는 원의 모서리까지의 직선 거리입니다. 기하학적 도형의 둘레와 동일하지만, 둘레라는 용어는 다각형에만 사용됩니다.
원의 둘레를 구하는 방법은?
원의 둘레 공식은 다음과 같습니다.
C = 2πr
여기서
- C는 원주입니다
- π(파이)는 대략 3.14159와 같은 수학 상수입니다.
- r은 원의 반지름이다
반지름은 원의 중심에서 가장자리의 임의의 점까지의 거리입니다.
지름은 반지름의 두 배이므로 원주는 다음과 같이 표현할 수도 있습니다.
C = πd
여기서
- d는 직경이다
예를 들어, 원의 반지름이 5cm이면 원주는 다음과 같습니다.
C = 2πr = 2π * 5 cm = 10π cm
≈ 31.4cm (소수점 둘째 자리까지 반올림)
AhaSlides의 추가 팁
- 수업 중 재미있는 연습을 위한 70개 이상의 수학 퀴즈 질문
- 지루한 K10 학생들을 위한 최고의 교실 수학 게임 12가지
- 성인용 두뇌 티저에 대한 60가지 멋진 아이디어 | 2023 업데이트
AhaSlides는 최고의 퀴즈 메이커입니다
지루함을 없애기 위해 광범위한 템플릿 라이브러리를 사용하여 즉시 대화형 게임을 만들어 보세요.
원의 둘레 퀴즈
질문 1: 원형 수영장의 둘레가 50m라면 반지름은 얼마입니까?
A. 7.95미터
나. 8.00미터
C. 15.91미터
D. 25미터
✅ 정답 :
A. 7.95미터
설명 :
반지름은 공식 C = 2πr을 재배열하고 r에 대해 풀면 구할 수 있습니다: r = C / (2π). 주어진 원주 50미터를 대입하고 π를 3.14로 근사하면 반지름은 약 7.95미터입니다.
질문 2: 원의 지름은 14인치입니다. 반지름은 얼마입니까?
A. 28인치
B.14인치
C. 21인치
D.7인치
✅ 정답 :
D.7인치
설명 :
지름은 반지름의 길이의 두 배이므로(d = 2r), 지름을 2로 나누면 반지름을 구할 수 있습니다(r = d / 2). 이 경우, 주어진 지름 14인치를 2로 나누면 반지름은 7인치가 됩니다.
질문 3: 원의 지름과 둘레의 관계에 대한 다음 진술 중 어느 것이 사실입니까?
A. 지름은 원주 길이의 절반입니다.
B. 지름은 원주와 같습니다.
C. 지름은 원주 길이의 두 배입니다.
D. 지름은 원주 길이의 π배입니다.
✅ 정답 :
A. 지름은 원주 길이의 절반입니다.
설명 :
지름은 반지름의 2배이고, 원주는 반지름의 2π배입니다. 따라서 지름은 원주의 절반입니다.
질문 4: 우리가 앉을 테이블의 둘레는 6.28야드입니다. 테이블의 지름을 구해야 합니다.
A. 1야드
B. 2야드
C. 3야드
D. 4야드
✅ 정답 :
B. 2야드
설명 :
원의 둘레는 지름에 파이(π)를 곱하여 계산합니다. 이 경우 둘레는 6.28야드입니다. 지름을 구하려면 둘레를 파이로 나누어야 합니다. 6.28야드를 파이로 나누면 약 2야드가 됩니다. 따라서 테이블의 지름은 2야드입니다.
질문 5: 원형 정원의 둘레는 36미터입니다. 정원의 대략적인 반지름은 얼마입니까?
A. 3.14미터
나. 6미터
C. 9미터
D. 18미터
✅ 정답 :
C. 9미터
설명 :
반지름을 구하려면 원주 공식을 사용하세요: C = 2πr. 공식을 다시 정리하여 반지름을 구하세요: r = C / (2π). 주어진 원주 36미터를 대입하고 π의 근사값을 3.14로 하면 r = 36 / (2 * 3.14) ≈ 9미터가 됩니다.
질문 6: 원형 수영장의 반지름이 8m입니다. 수영자가 수영장을 한 바퀴 도는 데 걸리는 대략적인 거리는 얼마입니까?
A. 16미터
나. 25미터
C. 50미터
D. 100미터
✅ 정답 :
C. 50미터
설명 :
수영 선수가 수영장을 한 바퀴 도는 거리를 구하려면 원주 공식(C = 2πr)을 사용합니다. 이 경우, 원주 공식은 2 * 3.14 * 8m = 50.24m로, 약 50m입니다.
질문 7: 수업 시간에 훌라후프를 측정했을 때, C조는 훌라후프의 반지름이 7인치라는 것을 발견했습니다. 훌라후프의 둘레는 얼마입니까?
A. 39.6인치
B. 37.6인치
C. 47.6인치
D.49.6인치
✅ 정답 :
C. 47.6인치
설명 :
원의 둘레는 C = 2πr 공식을 사용하여 구할 수 있습니다. 여기서 r은 원의 반지름입니다. 이 경우 훌라후프의 반지름은 7인치입니다. 이 값을 공식에 대입하면 C = 2π(7) = 14π인치가 됩니다. π를 3.14로 근사하면 둘레는 14(3.14) = 43.96인치가 됩니다. 소수점 첫째 자리까지 반올림하면 둘레는 47.6인치로, 주어진 답과 일치합니다.
질문 8: 반지름이 10m인 반원의 둘레는 얼마입니까?
A. 20미터
나. 15미터
C. 31.42미터
D. 62.84미터
✅ 정답 :
C. 31.42미터
설명 : 반원의 둘레를 구하려면 반지름이 10m인 원의 둘레의 절반을 계산합니다.
질문 9: 농구팀은 반지름이 5.6인치인 공을 가지고 경기합니다. 각 농구공의 둘레는 얼마입니까?
A. 11.2인치
B. 17.6인치
C. 22.4인치
D.35.2인치
✅ 정답 :
C. 22.4인치
설명:
원의 둘레 공식은 C = 2πr입니다. 주어진 반지름은 5.6인치입니다. 이 값을 공식에 대입하면 C = 2π * 5.6인치가 됩니다. C ≈ 2 * 3.14 * 5.6인치. C ≈ 11.2 * 5.6인치. C ≈ 22.4인치. 따라서 각 농구공의 둘레는 약 22.4인치입니다. 이는 농구공 둘레의 길이를 나타냅니다.
질문 10: 사라와 두 친구는 모임을 위해 원형 피크닉 테이블을 만들고 있었습니다. 모두가 편안하게 앉으려면 테이블 둘레가 18피트(약 XNUMXm)가 되어야 한다는 것을 알고 있었습니다. 적절한 둘레를 얻으려면 피크닉 테이블의 지름은 얼마여야 할까요?
A. 3피트
B. 6피트
C. 9피트
D. 12피트
✅ 정답 :
B. 6피트
설명 :
반지름을 구하려면 원주를 2π로 나누면 r = C / (2π) r = 18 피트 / (2 * 3.14) r ≈ 18 피트 / 6.28 r ≈ 2.87 피트(가장 가까운 백분의 일 자리로 반올림)가 됩니다.
이제 지름을 구하려면 반지름을 두 배로 하면 됩니다. 지름 = 2 * 반지름 지름 ≈ 2 * 2.87피트 지름 ≈ 5.74피트. 따라서 피크닉 테이블의 지름은 약 5.74피트여야 합니다.
주요 테이크 아웃
아하 슬라이드 교육, 훈련 또는 엔터테인먼트 목적으로 사용할 수 있는 최고의 인터랙티브 퀴즈 제작 도구입니다. 지금 바로 AhaSlides를 무료로 사용해 보세요. 맞춤형 템플릿 그리고 고급 기능!
자주 묻는 질문들 (FAQ)
원의 2πr은 무엇입니까?
2πr은 원의 둘레를 나타내는 공식입니다. 이 공식에서:
- "2"는 반지름 길이의 두 배를 의미합니다. 원주는 원 둘레의 길이이므로 원을 한 바퀴 돌고 다시 한 바퀴 돌아야 하므로 2를 곱합니다.
- "π"(파이)는 약 3.14159에 해당하는 수학 상수입니다. 원의 둘레와 지름 사이의 관계를 나타내기 때문에 사용됩니다.
- "r"은 원의 반지름을 나타내는데, 이는 원의 중심에서 원주상의 임의의 점까지의 거리를 말합니다.
왜 원주는 2πr인가요?
원의 둘레 공식 C = 2πr은 파이(π)의 정의와 원의 기하학적 특성에서 유래합니다. 파이(π)는 원의 둘레와 지름의 비율을 나타냅니다. 반지름(r)에 2π를 곱하면 원 둘레의 길이가 계산되는데, 이것이 바로 원의 둘레의 정의입니다.
원주는 반지름의 3.14배입니까?
아니요, 원둘레는 반지름의 3.14배가 아닙니다. 원둘레와 반지름 사이의 관계는 C = 2πr 공식으로 주어집니다. π(파이)는 약 3.14159이지만, 원둘레는 반지름의 2배 π배입니다. 따라서 원둘레는 반지름의 3.14배가 아니라 반지름의 2배 π배입니다.
