Hoe bereken je de omtrek van een cirkel precies?
De omtrek van een cirkel is een basiskennis van wiskunde die vereist is op de basisschool of middelbare school. Het beheersen van de omtrek van een cirkel is essentieel voor leerlingen die van plan zijn om geavanceerdere wiskundevakken te volgen op de middelbare school en universiteit en zich willen voorbereiden op gestandaardiseerde examens zoals de SAT en ACT.
De quiz over de omtrek van een cirkel in dit artikel is bedoeld om te testen in hoeverre u de straal, diameter en omtrek van een cirkel begrijpt.
Inhoudsopgave:
- Formule voor de omtrek van een cirkel
- Quiz over de omtrek van een cirkel
- Key afhaalrestaurants
- Veelgestelde Vragen / FAQ
Formule voor de omtrek van een cirkel
Voordat u een test doet, willen we nog even wat belangrijke informatie samenvatten!
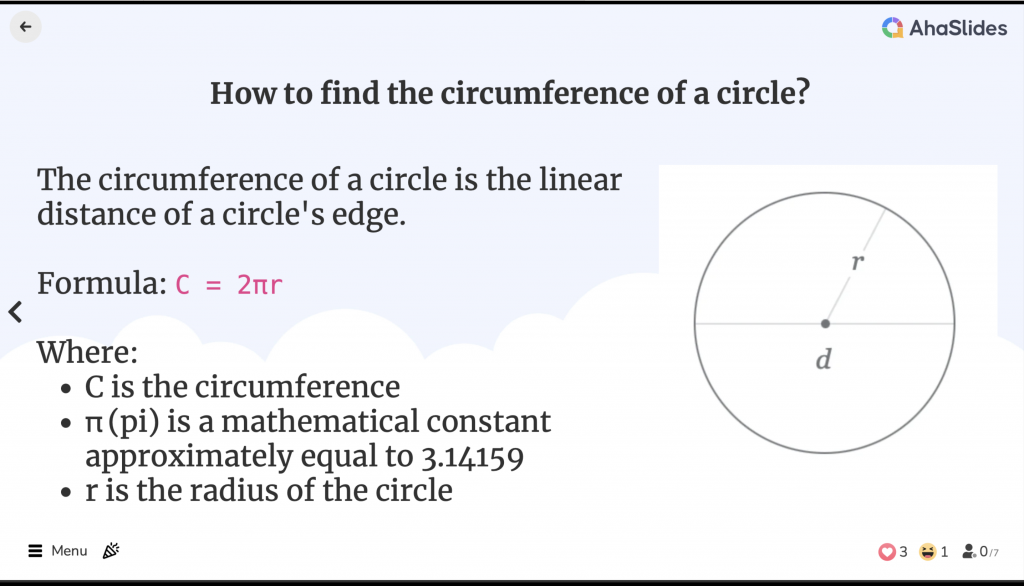
Wat is de omtrek van een cirkel?
De omtrek van een cirkel is de lineaire afstand van de rand van een cirkel. Het is gelijk aan de omtrek van een geometrische vorm, hoewel de term omtrek alleen wordt gebruikt voor veelhoeken.
Hoe bepaal je de omtrek van een cirkel?
De formule voor de omtrek van een cirkel is:
C = 2πr
waar:
- C is de omtrek
- π (pi) is een wiskundige constante die ongeveer gelijk is aan 3.14159
- r is de straal van de cirkel
De straal is de afstand van het middelpunt van de cirkel tot een willekeurig punt op de rand.
De diameter is tweemaal de straal, dus de omtrek kan ook als volgt worden uitgedrukt:
C = πd
waar:
- d is de diameter
Als de straal van een cirkel bijvoorbeeld 5 cm is, dan is de omtrek:
C = 2πr = 2π * 5 cm = 10π cm
≈ 31.4 cm (afgerond op 2 decimalen)
Meer tips van AhaSlides
- 70+ wiskundequizvragen voor leuke oefeningen in de klas
- 10 beste wiskundegames in de klas voor verveelde K12-studenten
- 60 geweldige ideeën over hersenkrakers voor volwassenen | 2023-updates
AhaSlides is de ultieme quizmaker
Maak in een handomdraai interactieve games met onze uitgebreide sjabloonbibliotheek om de verveling tegen te gaan
Quiz over de omtrek van een cirkel
Vraag 1: Als de omtrek van een rond zwembad 50 meter is, wat is dan de straal?
A. 7.95 meter
B. 8.00 meter
C. 15.91 meter
D. 25 meter
✅ Goed antwoord:
A. 7.95 meter
Uitleg:
De straal kan worden gevonden door de formule C = 2πr te herschikken en r op te lossen: r = C / (2π). Door de gegeven omtrek van 50 meter in te vullen en π te benaderen met 3.14, vinden we de straal ongeveer 7.95 meter.
Vraag 2: De diameter van een cirkel is 14 inch. Wat is de straal?
A. 28 inch
B.14 inch
C. 21 inch
D. 7 inch
✅ Goed antwoord:
D. 7 inch
Uitleg:
Omdat de diameter twee keer zo groot is als de straal (d = 2r), kun je de straal vinden door de diameter te delen door 2 (r = d / 2). In dit geval krijg je een straal van 7 inch als je de gegeven diameter van 14 inch deelt door 2.
Vraag 3: Welke van de volgende beweringen over de relatie tussen de diameter en de omtrek van een cirkel is waar?
A. De diameter is de helft van de omtrek.
B. De diameter is gelijk aan de omtrek.
C. De diameter is tweemaal de omtrek.
D. De diameter is π maal de omtrek.
✅ Goed antwoord:
A. De diameter is de helft van de omtrek.
Uitleg:
De diameter is gelijk aan 2 keer de straal, terwijl de omtrek gelijk is aan 2π keer de straal. De diameter is dus de helft van de omtrek.
Vraag 4: De tafel waaraan we moeten zitten heeft een omtrek van 6.28 yards. We moeten de diameter van de tafel bepalen.
A. 1 yard
B. 2 meter
C. 3 meter
D. 4 meter
✅ Goed antwoord:
B. 2 meter
Uitleg:
De omtrek van een cirkel wordt berekend door de diameter te vermenigvuldigen met pi (π). In dit geval is de omtrek 6.28 yards. Om de diameter te vinden, moeten we de omtrek delen door pi. 6.28 yards delen door pi geeft ons ongeveer 2 yards. De diameter van de tafel is dus 2 yards.
Vraag 5: Een cirkelvormige tuin heeft een omtrek van 36 meter. Wat is ongeveer de straal van de tuin?
A. 3.14 meter
B. 6 meter
C. 9 meter
D. 18 meter
✅ Goed antwoord:
C. 9 meter
Uitleg:
Om de straal te vinden, gebruik je de formule voor omtrek: C = 2πr. Herschik de formule om de straal te berekenen: r = C / (2π). Door de gegeven omtrek van 36 meter in te vullen en een geschatte waarde van π te gebruiken van 3.14, krijg je r = 36 / (2 * 3.14) ≈ 9 meter.
Vraag 6: Een rond zwembad heeft een straal van 8 meter. Wat is de geschatte afstand die een zwemmer aflegt om één baantje te zwemmen?
A. 16 meter
B. 25 meter
C. 50 meter
D. 100 meter
✅ Goed antwoord:
C. 50 meter
Uitleg:
Om de afstand te berekenen die een zwemmer in één baan rond het zwembad aflegt, gebruik je de omtrekformule (C = 2πr). In dit geval is dat 2 * 3.14 * 8 meter ≈ 50.24 meter, wat ongeveer 50 meter is.
Vraag 7: Bij het opmeten van de hoelahoep in de klas ontdekte groep C dat deze een straal van 7 cm had. Wat is de omtrek van de hoelahoep?
A. 39.6 inch
B. 37.6 inch
C. 47.6 inch
D. 49.6 inch
✅ Goed antwoord:
C. 47.6 inch
Uitleg:
De omtrek van een cirkel kan worden gevonden met de formule C = 2πr, waarbij r de straal van de cirkel is. In dit geval is de straal van de hoelahoep 7 inch. Door deze waarde in de formule in te vullen, krijgen we C = 2π(7) = 14π inch. Door π te benaderen met 3.14, kunnen we de omtrek berekenen als 14(3.14) = 43.96 inch. Afgerond op de dichtstbijzijnde tiende is de omtrek 47.6 inch, wat overeenkomt met het gegeven antwoord.
Vraag 8: Een halve cirkel heeft een straal van 10 meter. Wat is de omtrek?
A. 20 meter
B. 15 meter
C. 31.42 meter
D. 62.84 meter
✅ Goed antwoord:
C. 31.42 meter
Uitleg: Om de omtrek van de halve cirkel te vinden, berekent u de helft van de omtrek van een volledige cirkel met een straal van 10 meter.
Vraag 9: Het basketbalteam speelt met een bal met een straal van 5.6 inch. Wat is de omtrek van elke basketbal?
A. 11.2 inch
B. 17.6 inch
C. 22.4 inch
D. 35.2 inch
✅ Goed antwoord:
C. 22.4 inch
Uitleg:
Je kunt de formule voor de omtrek van een cirkel gebruiken, namelijk C = 2πr. De gegeven straal is 5.6 inch. Vul deze waarde in de formule in, we hebben C = 2π * 5.6 inch. C ≈ 2 * 3.14 * 5.6 inch. C ≈ 11.2 * 5.6 inch. C ≈ 22.4 inch. De omtrek van elke basketbal is dus ongeveer 22.4 inch. Dit is de afstand rond de basketbal.
Vraag 10: Sarah en haar twee vriendinnen waren bezig met het bouwen van een ronde picknicktafel voor hun bijeenkomst. Ze wisten dat ze een omtrek van 18 meter nodig hadden om er allemaal comfortabel rond te kunnen zitten. Welke diameter moet de picknicktafel hebben om de juiste omtrek te bereiken?
A. 3 voet
B. 6 voet
C. 9 voet
D. 12 voet
✅ Goed antwoord:
B. 6 voet
Uitleg:
Om de straal te vinden, deelt u de omtrek door 2π. We krijgen dan r = C / (2π) r = 18 voet / (2 * 3.14) r ≈ 18 voet / 6.28 r ≈ 2.87 voet (afgerond op de dichtstbijzijnde honderdste).
Om de diameter te vinden, verdubbelt u de straal: Diameter = 2 * Straal Diameter ≈ 2 * 2.87 voet Diameter ≈ 5.74 voet. De picknicktafel moet dus een diameter hebben van ongeveer 5.74 voet.
Key afhaalrestaurants
AhaDia's is de beste interactieve quizmaker die gebruikt kan worden voor educatieve, trainings- of entertainmentdoeleinden. Probeer AhaSlides meteen voor gratis aanpasbare sjablonen en geavanceerde functies!
Veelgestelde Vragen / FAQ
Wat is 2πr van een cirkel?
2πr is de formule voor de omtrek van een cirkel. In deze formule:
- "2" geeft aan dat je twee keer de lengte van de straal neemt. De omtrek is de afstand rond de cirkel, dus je moet de cirkel één keer rondgaan en dan nog een keer, daarom vermenigvuldigen we met 2.
- "π" (pi) is een wiskundige constante die ongeveer gelijk is aan 3.14159. Deze wordt gebruikt omdat hij de verhouding tussen de omtrek en de diameter van een cirkel weergeeft.
- “r” staat voor de straal van de cirkel, de afstand van het middelpunt van de cirkel tot een willekeurig punt op de omtrek.
Waarom is de omtrek 2πr?
De formule voor de omtrek van een cirkel, C = 2πr, is gebaseerd op de definitie van pi (π) en de geometrische eigenschappen van een cirkel. Pi (π) geeft de verhouding weer tussen de omtrek van een cirkel en zijn diameter. Wanneer je de straal (r) vermenigvuldigt met 2π, bereken je in feite de afstand rond de cirkel, wat de definitie van omtrek is.
Is de omtrek 3.14 keer de straal?
Nee, de omtrek is niet exact 3.14 keer de straal. De verhouding tussen de omtrek en de straal van een cirkel wordt gegeven door de formule C = 2πr. Terwijl π (pi) ongeveer 3.14159 is, is de omtrek 2 keer π keer de straal. De omtrek is dus meer dan 3.14 keer de straal; hij is 2 keer π keer de straal.
ref: Omni-calculator | Proprof
