Hur beräknar man exakt omkretsen av en cirkel?
Cirkelns omkrets är en grundläggande och obligatorisk matematikkunskap som introduceras i grundskolan eller mellanstadiet. Att behärska cirkelns omkrets är viktigt för elever som planerar att läsa mer avancerade matematikkurser på gymnasiet och högskolan och förbereda sig för standardiserade prov som SAT och ACT.
Quiz med 10 uppgifter om en cirkels omkrets i den här artikeln är utformat för att testa din förståelse för att hitta radien, diametern och omkretsen av en cirkel.
Innehåll:
Formel för cirkelns omkrets
Innan vi gör ett test, låt oss sammanfatta lite viktig information!
Vad är omkretsen av en cirkel?
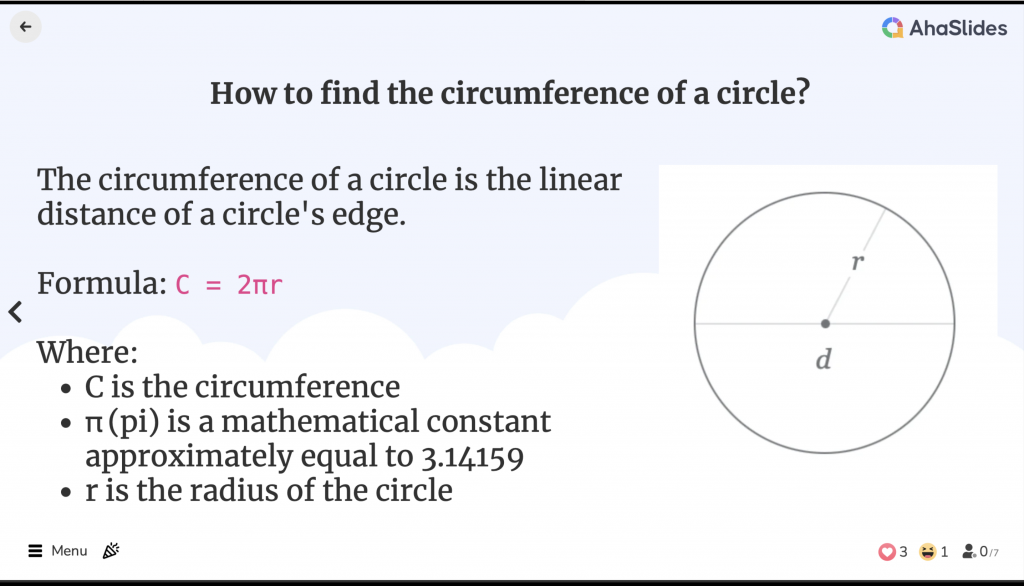
Omkretsen av en cirkel är det linjära avståndet för cirkelns kant. Den motsvarar omkretsen av en geometrisk form, även om termen omkrets endast används för polygoner.
Hur hittar man omkretsen av en cirkel?
Formeln för en cirkels omkrets är:
C = 2πr
där:
- C är omkretsen
- π (pi) är en matematisk konstant som är ungefär lika med 3.14159
- r är cirkelns radie
Radien är avståndet från cirkelns centrum till vilken punkt som helst på kanten.
Diametern är dubbelt så stor som radien, så omkretsen kan också uttryckas som:
C = πd
där:
- d är diametern
Om till exempel cirkelns radie är 5 cm, så är omkretsen:
C = 2πr = 2π * 5 cm = 10π cm
≈ 31.4 cm (avrundat till 2 decimaler)
Fler tips från AhaSlides
- 70+ Math Quiz-frågor för roliga övningar i klassen
- 10 bästa klassrumsmattespel för uttråkade K12-elever
- 60 fantastiska idéer om hjärntorn för vuxna | 2023-uppdateringar
AhaSlides är The Ultimate Quiz Maker
Gör interaktiva spel på ett ögonblick med vårt omfattande mallbibliotek för att döda tristess
Omkretsen av en cirkel frågesport
Fråga 1: Om omkretsen av en rund simbassäng är 50 meter, vad är dess radie?
A. 7.95 meter
B. 8.00 meter
C. 15.91 meter
D. 25 meter
✅ Rätt svar:
A. 7.95 meter
Förklaring:
Radien kan hittas genom att omformulera formeln C = 2πr och lösa för r: r = C / (2π). Om vi insätter den givna omkretsen på 50 meter och approximerar π till 3.14, finner vi att radien är ungefär 7.95 meter.
Fråga 2: Cirkelns diameter är 14 tum. Vad är dess radie?
A. 28 tum
B.14 tum
Ca 21 tum
D. 7 tum
✅ Rätt svar:
D. 7 tum
Förklaring:
Eftersom diametern är dubbelt så lång som radien (d = 2r), kan du hitta radien genom att dividera diametern med 2 (r = d / 2). I det här fallet ger en radie på 14 tum om man dividerar den givna diametern på 2 tum med 7.
Fråga 3: Vilket av följande påståenden är sant om förhållandet mellan diametern och omkretsen av en cirkel?
A. Diametern är halva omkretsen.
B. Diametern är densamma som omkretsen.
C. Diametern är dubbelt så stor som omkretsen.
D. Diametern är π gånger omkretsen.
✅ Rätt svar:
A. Diametern är halva omkretsen.
Förklaring:
Diametern är lika med 2 gånger radien, medan omkretsen är lika med 2π gånger radien. Därför är diametern hälften av omkretsen.
Fråga 4: Bordet vi ska sitta vid har en omkrets på 6.28 yards. Vi behöver hitta bordets diameter.
A. 1 yard
B. 2 yards
Ca 3 yards
D. 4 yards
✅ Rätt svar:
B. 2 yards
Förklaring:
Omkretsen av en cirkel beräknas genom att multiplicera diametern med pi (π). I detta fall anges omkretsen som 6.28 yards. För att hitta diametern måste vi dividera omkretsen med pi. Att dividera 6.28 yards med pi ger oss ungefär 2 yards. Därför är bordets diameter 2 yards.
Fråga 5: En cirkulär trädgård har en omkrets på 36 meter. Vad är trädgårdens ungefärliga radie?
A. 3.14 meter
B. 6 meter
C. 9 meter
D. 18 meter
✅ Rätt svar:
C. 9 meter
Förklaring:
För att hitta radien, använd formeln för omkrets: C = 2πr. Ordna om formeln för att lösa radien: r = C / (2π). Om du sätter in den givna omkretsen på 36 meter och använder ett ungefärligt värde på π som 3.14 får du r = 36 / (2 * 3.14) ≈ 9 meter.
Fråga 6: En rund simbassäng har en radie på 8 meter. Vilken ungefärlig sträcka tillryggalägger en simmare runt bassängen när han/hon simmar ett varv?
A. 16 meter
B. 25 meter
C. 50 meter
D. 100 meter
✅ Rätt svar:
C. 50 meter
Förklaring:
För att hitta sträckan en simmare tillryggalägger runt poolen under ett varv använder man omkretsformeln (C = 2πr). I det här fallet är det 2 * 3.14 * 8 meter ≈ 50.24 meter, vilket är ungefär 50 meter.
Fråga 7: När grupp C mätte hulahopringen i klassen upptäckte de att den hade en radie på 7 cm. Vad är hulahopringens omkrets?
A. 39.6 tum
B. 37.6 tum
Ca 47.6 tum
D. 49.6 tum
✅ Rätt svar:
Ca 47.6 tum
Förklaring:
Omkretsen av en cirkel kan beräknas med hjälp av formeln C = 2πr, där r är cirkelns radie. I detta fall anges hula-ringens radie som 7 tum. Om vi sätter in detta värde i formeln får vi C = 2π(7) = 14π tum. Om vi approximerar π till 3.14 kan vi beräkna omkretsen som 14(3.14) = 43.96 tum. Avrundat till närmaste tiondel är omkretsen 47.6 tum, vilket matchar det givna svaret.
Fråga 8: En halvcirkel har en radie på 10 meter. Vad är dess omkrets?
A. 20 meter
B. 15 meter
C. 31.42 meter
D. 62.84 meter
✅ Rätt svar:
C. 31.42 meter
Förklaring: För att hitta omkretsen av en halvcirkel, beräkna halva omkretsen av en hel cirkel med en radie på 10 meter.
Fråga 9: Basketlaget spelar med en boll med en radie på 5.6 tum. Vad är omkretsen på varje basketboll?
A. 11.2 tum
B. 17.6 tum
Ca 22.4 tum
D. 35.2 tum
✅ Rätt svar:
Ca 22.4 tum
Förklaring:
Du kan använda formeln för omkretsen av en cirkel, vilket är C = 2πr. Den givna radien är 5.6 tum. Sätt in detta värde i formeln, vi har C = 2π * 5.6 tum. C ≈ 2 * 3.14 * 5.6 tum. C ≈ 11.2 * 5.6 tum. C ≈ 22.4 tum. Så omkretsen av varje basketboll är ungefär 22.4 tum. Detta representerar avståndet runt basketbollen.
Fråga 10: Sarah och hennes två vänner byggde ett runt picknickbord för sin sammankomst. De visste att för att alla skulle kunna sitta bekvämt runt bordet behövde de en omkrets på 18 meter. Vilken diameter måste picknickbordet ha för att uppnå rätt omkrets?
A. 3 fot
B. 6 fot
Ca 9 fot
D. 12 fot
✅ Rätt svar:
B. 6 fot
Förklaring:
För att hitta radien, dividera omkretsen med 2π, vi har r = C / (2π) r = 18 fot / (2 * 3.14) r ≈ 18 fot / 6.28 r ≈ 2.87 fot (avrundat till närmaste hundradel).
För att hitta diametern, dubbla helt enkelt radien: Diameter = 2 * Radie Diameter ≈ 2 * 2.87 fot Diameter ≈ 5.74 fot. Så picknickbordet måste ha en diameter på ungefär 5.74 fot.
Viktiga takeaways
AhaSlides är den bästa interaktiva frågesportsverktyget som kan användas för utbildning, träning eller underhållning. Kolla in AhaSlides direkt för att få det gratis. anpassningsbara mallar och avancerade funktioner!
Vanliga frågor
Vad är 2πr av en cirkel?
2πr är formeln för omkretsen av en cirkel. I denna formel:
- "2" representerar att du tar dubbelt så lång radie. Omkretsen är avståndet runt cirkeln, så du måste gå runt cirkeln en gång och sedan igen, vilket är anledningen till att vi multiplicerar med 2.
- ”π” (pi) är en matematisk konstant som är ungefär lika med 3.14159. Den används eftersom den representerar förhållandet mellan omkretsen och diametern på en cirkel.
- "r" representerar cirkelns radie, vilket är avståndet från cirkelns centrum till vilken punkt som helst på dess omkrets.
Varför är omkretsen 2πr?
Formeln för en cirkels omkrets, C = 2πr, kommer från definitionen av pi (π) och cirkelns geometriska egenskaper. Pi (π) representerar förhållandet mellan cirkelns omkrets och dess diameter. När man multiplicerar radien (r) med 2π beräknar man i huvudsak avståndet runt cirkeln, vilket är definitionen av omkrets.
Är omkretsen 3.14 gånger radien?
Nej, omkretsen är inte exakt 3.14 gånger radien. Förhållandet mellan omkretsen och radien för en cirkel ges av formeln C = 2πr. Medan π (pi) är ungefär 3.14159, är omkretsen 2 gånger π gånger radien. Så omkretsen är mer än bara 3.14 gånger radien; den är 2 gånger π gånger radien.
Ref: Omni Caculator | Prof
