Hvordan beregner man præcist omkredsen af en cirkel?
Omkredsen af en cirkel er en grundlæggende og obligatorisk matematikviden, der introduceres i folkeskolen eller mellemtrinnet. At mestre omkredsen af en cirkel er afgørende for elever, der planlægger at tage mere avancerede matematikkurser i gymnasiet og på universitetet og forberede sig til standardiserede eksamener som SAT og ACT.
Quiz med 10 spørgsmål om en cirkels omkreds i denne artikel er designet til at teste din forståelse af at finde radius, diameter og omkreds af en cirkel.
Indholdsfortegnelse:
- Formel for omkreds af en cirkel
- Omkredsen af en cirkel quiz
- Vigtige takeaways
- Ofte stillede spørgsmål
Formel for omkreds af en cirkel
Før vi tager en test, lad os opsummere nogle vigtige oplysninger!
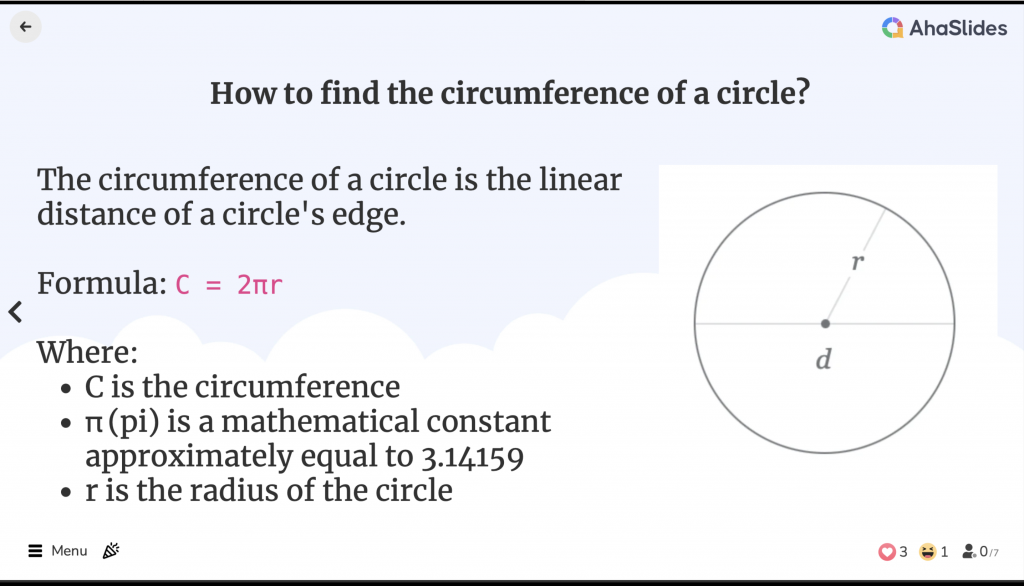
Hvad er omkredsen af en cirkel?
Omkredsen af en cirkel er den lineære afstand af cirklens kant. Den svarer til omkredsen af en geometrisk form, selvom udtrykket omkreds kun bruges om polygoner.
Hvordan finder man omkredsen af en cirkel?
Formlen for en cirkels omkreds er:
C = 2πr
hvor:
- C er omkredsen
- π (pi) er en matematisk konstant, der er omtrent lig med 3.14159
- r er cirklens radius
Radius er afstanden fra cirklens centrum til ethvert punkt på kanten.
Diameteren er dobbelt så stor som radius, så omkredsen kan også udtrykkes som:
C = πd
hvor:
- d er diameteren
Hvis for eksempel radiusen af en cirkel er 5 cm, så er omkredsen:
C = 2πr = 2π * 5 cm = 10π cm
≈ 31.4 cm (afrundet til 2 decimaler)
Flere tips fra AhaSlides
- 70+ matematikquizspørgsmål til sjove øvelser i klassen
- 10 bedste matematikspil i klasseværelset for kede K12-elever
- 60 fantastiske ideer til hjernevridere for voksne | 2023-opdateringer
AhaSlides er The Ultimate Quiz Maker
Lav interaktive spil på et øjeblik med vores omfattende skabelonbibliotek for at dræbe kedsomhed
Omkredsen af en cirkel quiz
Spørgsmål 1: Hvis omkredsen af en cirkulær swimmingpool er 50 meter, hvad er så dens radius?
A. 7.95 meter
B. 8.00 meter
C. 15.91 meter
D. 25 meter
✅ Rigtigt svar:
A. 7.95 meter
Forklaring:
Radius kan findes ved at omarrangere formlen C = 2πr og løse for r: r = C / (2π). Ved at indsætte den givne omkreds på 50 meter og approksimere π til 3.14, finder vi radius til at være cirka 7.95 meter.
Spørgsmål 2: Diameteren af en cirkel er 14 tommer. Hvad er dens radius?
A. 28 tommer
B.14 tommer
Ca. 21 tommer
D. 7 tommer
✅ Rigtigt svar:
D. 7 tommer
Forklaring:
Da diameteren er dobbelt så lang som radius (d = 2r), kan du finde radius ved at dividere diameteren med 2 (r = d / 2). I dette tilfælde giver dividering af den givne diameter på 14 tommer med 2 en radius på 7 tommer.
Spørgsmål 3: Hvilket af følgende udsagn er sandt om forholdet mellem diameteren og omkredsen af en cirkel?
A. Diameteren er halvdelen af omkredsen.
B. Diameteren er den samme som omkredsen.
C. Diameteren er dobbelt så stor som omkredsen.
D. Diameteren er π gange omkredsen.
✅ Rigtigt svar:
A. Diameteren er halvdelen af omkredsen.
Forklaring:
Diameteren er lig med 2 gange radius, mens omkredsen er lig med 2π gange radius. Derfor er diameteren halvdelen af omkredsen.
Spørgsmål 4: Bordet, vi skal sidde ved, har en omkreds på 6.28 yards. Vi skal finde bordets diameter.
A. 1 yard
B. 2 yards
Ca. 3 yards
D. 4 yards
✅ Rigtigt svar:
B. 2 yards
Forklaring:
Omkredsen af en cirkel beregnes ved at gange diameteren med pi (π). I dette tilfælde er omkredsen angivet som 6.28 yards. For at finde diameteren skal vi dividere omkredsen med pi. Ved at dividere 6.28 yards med pi får vi cirka 2 yards. Derfor er bordets diameter 2 yards.
Spørgsmål 5: En cirkulær have har en omkreds på 36 meter. Hvad er havens omtrentlige radius?
A. 3.14 meter
B. 6 meter
C. 9 meter
D. 18 meter
✅ Rigtigt svar:
C. 9 meter
Forklaring:
For at finde radius skal du bruge formlen for omkreds: C = 2πr. Omarranger formlen for at finde radius: r = C / (2π). Ved at indsætte den givne omkreds på 36 meter og bruge en omtrentlig værdi af π som 3.14, får du r = 36 / (2 * 3.14) ≈ 9 meter.
Spørgsmål 6: En cirkulær swimmingpool har en radius på 8 meter. Hvad er den omtrentlige afstand, en svømmer tilbagelægger rundt om poolen, når han gennemfører en omgang?
A. 16 meter
B. 25 meter
C. 50 meter
D. 100 meter
✅ Rigtigt svar:
C. 50 meter
Forklaring:
For at finde den afstand, en svømmer tilbagelægger rundt om poolen på én omgang, bruger du omkredsformlen (C = 2πr). I dette tilfælde er det 2 * 3.14 * 8 meter ≈ 50.24 meter, hvilket er cirka 50 meter.
Spørgsmål 7: Da gruppe C målte hulahopringen i klassen, opdagede de, at den havde en radius på 7 cm. Hvad er hulahopringens omkreds?
A. 39.6 tommer
B. 37.6 tommer
Ca. 47.6 tommer
D. 49.6 tommer
✅ Rigtigt svar:
Ca. 47.6 tommer
Forklaring:
Omkredsen af en cirkel kan findes ved hjælp af formlen C = 2πr, hvor r er cirklens radius. I dette tilfælde er hulahopringens radius angivet som 7 tommer. Ved at indsætte denne værdi i formlen får vi C = 2π(7) = 14π tommer. Ved at tilnærme π til 3.14 kan vi beregne omkredsen som 14(3.14) = 43.96 tommer. Afrundet til nærmeste tiendedel er omkredsen 47.6 tommer, hvilket matcher det givne svar.
Spørgsmål 8: En halvcirkel har en radius på 10 meter. Hvad er dens omkreds?
A. 20 meter
B. 15 meter
C. 31.42 meter
D. 62.84 meter
✅ Rigtigt svar:
C. 31.42 meter
Forklaring: For at finde omkredsen af en halvcirkel skal du beregne halvdelen af omkredsen af en fuld cirkel med en radius på 10 meter.
Spørgsmål 9: Basketballholdet spiller med en bold med en radius på 5.6 tommer. Hvad er omkredsen af hver basketball?
A. 11.2 tommer
B. 17.6 tommer
Ca. 22.4 tommer
D. 35.2 tommer
✅ Rigtigt svar:
Ca. 22.4 tommer
Forklaring:
Du kan bruge formlen for omkredsen af en cirkel, som er C = 2πr. Den givne radius er 5.6 tommer. Indsæt denne værdi i formlen, vi har C = 2π * 5.6 tommer. C ≈ 2 * 3.14 * 5.6 tommer. C ≈ 11.2 * 5.6 tommer. C ≈ 22.4 tommer. Så omkredsen af hver basketball er cirka 22.4 tommer. Dette repræsenterer afstanden omkring basketballen.
Spørgsmål 10: Sarah og hendes to venner byggede et rundt picnicbord til deres sammenkomst. De vidste, at for at de alle kunne sidde komfortabelt omkring bordet, skulle de have en omkreds på 18 meter. Hvilken diameter skal picnicbordet have for at opnå den korrekte omkreds?
A. 3 fod
B. 6 fod
Ca. 9 fod
D. 12 fod
✅ Rigtigt svar:
B. 6 fod
Forklaring:
For at finde radiusen divideres omkredsen med 2π. Vi har r = C / (2π) r = 18 fod / (2 * 3.14) r ≈ 18 fod / 6.28 r ≈ 2.87 fod (afrundet til nærmeste hundrededel).
For at finde diameteren skal du blot fordoble radius: Diameter = 2 * Radius Diameter ≈ 2 * 2.87 fod Diameter ≈ 5.74 fod. Så picnicbordet skal have en diameter på cirka 5.74 fod.
Vigtige takeaways
AhaSlides er den bedste interaktive quiz-maskine, der kan bruges til uddannelse, træning eller underholdning. Tjek AhaSlides ud med det samme for at få det gratis. tilpasselige skabeloner og avancerede funktioner!
Ofte stillede spørgsmål
Hvad er 2πr af en cirkel?
2πr er formlen for omkredsen af en cirkel. I denne formel:
- "2" repræsenterer, at du tager dobbelt så lang radius. Omkredsen er afstanden rundt om cirklen, så du skal gå rundt om cirklen én gang og derefter igen, hvilket er grunden til, at vi ganger med 2.
- "π" (pi) er en matematisk konstant, der er omtrent lig med 3.14159. Den bruges, fordi den repræsenterer forholdet mellem omkredsen og diameteren af en cirkel.
- "r" repræsenterer cirklens radius, som er afstanden fra cirklens centrum til ethvert punkt på dens omkreds.
Hvorfor er omkredsen 2πr?
Formlen for en cirkels omkreds, C = 2πr, stammer fra definitionen af pi (π) og de geometriske egenskaber ved en cirkel. Pi (π) repræsenterer forholdet mellem en cirkels omkreds og dens diameter. Når man ganger radius (r) med 2π, beregner man i bund og grund afstanden omkring cirklen, hvilket er definitionen af omkreds.
Er omkredsen 3.14 gange radius?
Nej, omkredsen er ikke præcis 3.14 gange radius. Forholdet mellem omkredsen og radius af en cirkel er givet ved formlen C = 2πr. Mens π (pi) er omtrent 3.14159, er omkredsen 2 gange π gange radius. Så omkredsen er mere end blot 3.14 gange radius; den er 2 gange π gange radius.
ref: Omni Caculator | Prof
