Wie berechnet man den Umfang eines Kreises genau?
Der Kreisumfang ist eine grundlegende und notwendige mathematische Kenntnis, die in der Grundschule oder Mittelschule vermittelt wird. Die Beherrschung des Kreisumfangs ist unerlässlich für Schüler, die in der Oberstufe und am College fortgeschrittene Mathematikkurse belegen und sich auf standardisierte Prüfungen wie SAT und ACT vorbereiten möchten.
Das Quiz „10 Kreisumfänge“ in diesem Artikel soll Ihr Wissen zum Berechnen von Radius, Durchmesser und Umfang eines Kreises testen.
Table of Contents:
Umfang einer Kreisformel
Bevor wir einen Test machen, fassen wir einige wichtige Informationen zusammen!
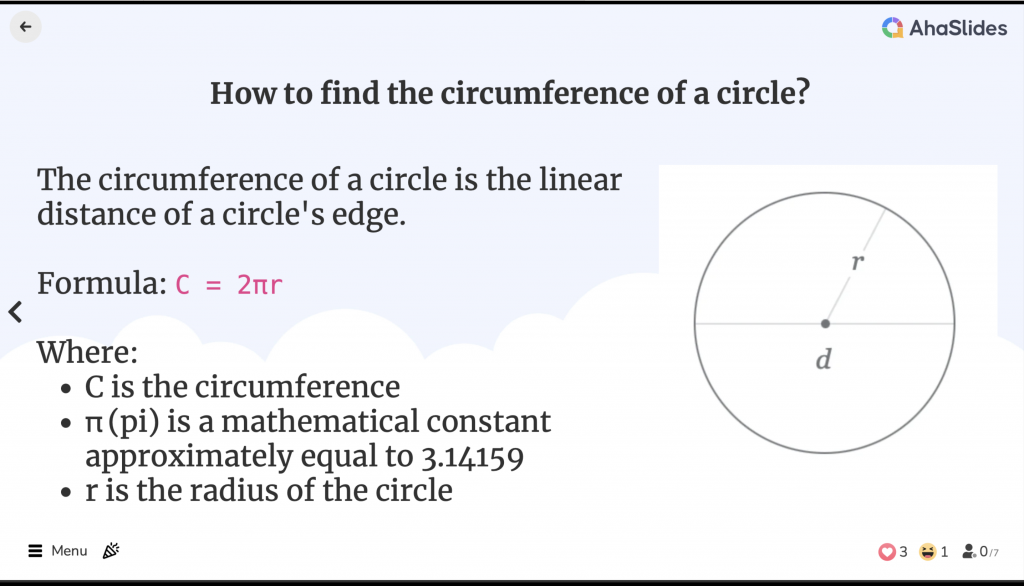
Wie groß ist der Umfang eines Kreises?
Der Umfang eines Kreises ist die lineare Entfernung der Kreiskante. Er entspricht dem Umfang einer geometrischen Form, wobei der Begriff Umfang nur für Polygone verwendet wird.
Wie berechnet man den Umfang eines Kreises?
Die Formel für den Umfang eines Kreises lautet:
C = 2πr
wo:
- C ist der Umfang
- π (Pi) ist eine mathematische Konstante, die ungefähr 3.14159 entspricht
- r ist der Radius des Kreises
Der Radius ist der Abstand vom Mittelpunkt des Kreises zu einem beliebigen Punkt am Rand.
Der Durchmesser ist doppelt so groß wie der Radius, daher kann der Umfang auch wie folgt ausgedrückt werden:
C = πd
wo:
- d ist der Durchmesser
Wenn beispielsweise der Radius eines Kreises 5 cm beträgt, dann ist der Umfang:
C = 2πr = 2π * 5 cm = 10π cm
≈ 31.4 cm (auf 2 Dezimalstellen gerundet)
Weitere Tipps von AhaSlides
- Über 70 Mathe-Quizfragen für lustige Übungen im Unterricht
- Die 10 besten Mathe-Klassenspiele für gelangweilte K12-Schüler
- 60 tolle Ideen zu Denksportaufgaben für Erwachsene | 2023-Updates
AhaSlides ist der ultimative Quiz-Maker
Erstellen Sie mit unserer umfangreichen Vorlagenbibliothek im Handumdrehen interaktive Spiele, um Langeweile zu vertreiben
Quiz zum Umfang eines Kreises
Frage 1: Wenn der Umfang eines runden Schwimmbeckens 50 Meter beträgt, wie groß ist dann sein Radius?
A. 7.95 Meter
B. 8.00 Meter
C. 15.91 Meter
D. 25 Meter
✅ Richtige Antwort:
A. 7.95 Meter
Erläuterung:
Der Radius lässt sich berechnen, indem man die Formel C = 2πr umstellt und nach r auflöst: r = C / (2π). Wenn wir den gegebenen Umfang von 50 Metern einsetzen und π auf 3.14 approximieren, erhalten wir einen Radius von etwa 7.95 Metern.
Frage 2: Der Durchmesser eines Kreises beträgt 14 Zoll. Wie groß ist sein Radius?
A. 28 Zoll
B.14 Zoll
Ca. 21 Zoll
D. 7 Zoll
✅ Richtige Antwort:
D. 7 Zoll
Erläuterung:
Da der Durchmesser doppelt so lang ist wie der Radius (d = 2r), können Sie den Radius ermitteln, indem Sie den Durchmesser durch 2 teilen (r = d / 2). In diesem Fall ergibt die Division des gegebenen Durchmessers von 14 Zoll durch 2 einen Radius von 7 Zoll.
Frage 3: Welche der folgenden Aussagen über die Beziehung zwischen Durchmesser und Umfang eines Kreises ist richtig?
A. Der Durchmesser ist die Hälfte des Umfangs.
B. Der Durchmesser ist gleich dem Umfang.
C. Der Durchmesser ist doppelt so groß wie der Umfang.
D. Der Durchmesser ist π mal der Umfang.
✅ Richtige Antwort:
A. Der Durchmesser ist die Hälfte des Umfangs.
Erläuterung:
Der Durchmesser entspricht dem 2-fachen Radius, während der Umfang dem 2π-fachen Radius entspricht. Daher ist der Durchmesser halb so groß wie der Umfang.
Frage 4: Der Tisch, an dem wir sitzen müssen, hat einen Umfang von 6.28 Metern. Wir müssen den Durchmesser des Tisches ermitteln.
A. 1 Yard
B. 2 Yards
C. 3 Yards
D. 4 Meter
✅ Richtige Antwort:
B. 2 Yards
Erläuterung:
Der Umfang eines Kreises wird berechnet, indem der Durchmesser mit Pi (π) multipliziert wird. In diesem Fall beträgt der Umfang 6.28 Yards. Um den Durchmesser zu ermitteln, müssen wir den Umfang durch Pi teilen. 6.28 Yards geteilt durch Pi ergeben ungefähr 2 Yards. Der Durchmesser des Tisches beträgt also 2 Yards.
Frage 5: Ein kreisförmiger Garten hat einen Umfang von 36 Metern. Wie groß ist der ungefähre Radius des Gartens?
A. 3.14 Meter
B. 6 Meter
C. 9 Meter
D. 18 Meter
✅ Richtige Antwort:
C. 9 Meter
Erläuterung:
Um den Radius zu berechnen, verwenden Sie die Formel für den Umfang: C = 2πr. Um den Radius zu berechnen, formulieren Sie die Formel um: r = C / (2π). Setzen wir den gegebenen Umfang von 36 Metern ein und verwenden wir einen Näherungswert von π von 3.14, erhalten wir r = 36 / (2 * 3.14) ≈ 9 Meter.
Frage 6: Ein rundes Schwimmbecken hat einen Radius von 8 Metern. Wie weit legt ein Schwimmer ungefähr eine Runde im Becken zurück?
A. 16 Meter
B. 25 Meter
C. 50 Meter
D. 100 Meter
✅ Richtige Antwort:
C. 50 Meter
Erläuterung:
Um die Distanz zu berechnen, die ein Schwimmer bei einer Runde im Becken zurücklegt, verwendet man die Umfangsformel (C = 2πr). In diesem Fall beträgt sie 2 * 3.14 * 8 Meter ≈ 50.24 Meter, also ungefähr 50 Meter.
Frage 7: Beim Messen des Hula-Hoop-Reifens im Unterricht stellte Gruppe C fest, dass dieser einen Radius von 7 cm hatte. Wie groß ist der Umfang des Hula-Hoop-Reifens?
A. 39.6 Zoll
B. 37.6 Zoll
Ca. 47.6 Zoll
D. 49.6 Zoll
✅ Richtige Antwort:
Ca. 47.6 Zoll
Erläuterung:
Der Umfang eines Kreises lässt sich mit der Formel C = 2πr berechnen, wobei r der Radius des Kreises ist. In diesem Fall beträgt der Radius des Hula-Hoop-Reifens 7 Zoll. Setzen wir diesen Wert in die Formel ein, erhalten wir C = 2π(7) = 14π Zoll. Wenn wir π auf 3.14 approximieren, erhalten wir den Umfang als 14(3.14) = 43.96 Zoll. Auf die nächste Zehntelstelle gerundet ergibt sich ein Umfang von 47.6 Zoll, was dem gegebenen Ergebnis entspricht.
Frage 8: Ein Halbkreis hat einen Radius von 10 Metern. Wie groß ist sein Umfang?
A. 20 Meter
B. 15 Meter
C. 31.42 Meter
D. 62.84 Meter
✅ Richtige Antwort:
C. 31.42 Meter
Erläuterung: Um den Umfang des Halbkreises zu ermitteln, berechnen Sie den halben Umfang eines Vollkreises mit einem Radius von 10 Metern.
Frage 9: Die Basketballmannschaft spielt mit einem Ball mit einem Radius von 5.6 Zoll. Wie groß ist der Umfang jedes Basketballs?
A. 11.2 Zoll
B. 17.6 Zoll
Ca. 22.4 Zoll
D. 35.2 Zoll
✅ Richtige Antwort:
Ca. 22.4 Zoll
Erläuterung:
Sie können die Formel für den Umfang eines Kreises verwenden: C = 2πr. Der gegebene Radius beträgt 5.6 Zoll. Setzen Sie diesen Wert in die Formel ein. Wir erhalten: C = 2π * 5.6 Zoll. C ≈ 2 * 3.14 * 5.6 Zoll. C ≈ 11.2 * 5.6 Zoll. C ≈ 22.4 Zoll. Der Umfang jedes Basketballs beträgt also ungefähr 22.4 Zoll. Dies stellt die Entfernung um den Basketball dar.
Frage 10: Sarah und ihre beiden Freundinnen bauten für ihr Treffen einen runden Picknicktisch. Sie wussten, dass sie einen Umfang von 18 Metern brauchten, damit alle bequem um den Tisch herumsitzen konnten. Welchen Durchmesser muss der Picknicktisch haben, um den richtigen Umfang zu erreichen?
A. 3 Fuß
B. 6 Fuß
C. 9 Fuß
D. 12 Fuß
✅ Richtige Antwort:
B. 6 Fuß
Erläuterung:
Um den Radius zu ermitteln, teilen Sie den Umfang durch 2π. Wir erhalten r = C / (2π) r = 18 Fuß / (2 * 3.14) r ≈ 18 Fuß / 6.28 r ≈ 2.87 Fuß (auf das nächste Hundertstel gerundet).
Um den Durchmesser zu ermitteln, verdoppeln Sie einfach den Radius: Durchmesser = 2 * Radius Durchmesser ≈ 2 * 2.87 Fuß Durchmesser ≈ 5.74 Fuß. Der Picknicktisch muss also einen Durchmesser von ungefähr 5.74 Fuß haben
Die zentralen Thesen
AhaFolien ist der beste interaktive Quiz-Maker, der für Bildungs-, Trainings- oder Unterhaltungszwecke verwendet werden kann. Schauen Sie sich AhaSlides gleich an, um kostenlos zu erhalten anpassbare Vorlagen und erweiterte Funktionen!
Häufig gestellte Fragen
Was ist 2πr eines Kreises?
2πr ist die Formel für den Umfang eines Kreises. In dieser Formel gilt:
- „2“ bedeutet, dass du die doppelte Länge des Radius nimmst. Der Umfang ist die Entfernung um den Kreis herum, du musst also einmal und dann noch einmal um den Kreis herumgehen, weshalb wir mit 2 multiplizieren.
- „π“ (Pi) ist eine mathematische Konstante, die ungefähr dem Wert 3.14159 entspricht. Sie wird verwendet, weil sie das Verhältnis zwischen Umfang und Durchmesser eines Kreises darstellt.
- „r“ stellt den Radius des Kreises dar, also die Entfernung vom Mittelpunkt des Kreises zu einem beliebigen Punkt auf seinem Umfang.
Warum beträgt der Umfang 2πr?
Die Formel für den Kreisumfang, C = 2πr, leitet sich von der Definition von Pi (π) und den geometrischen Eigenschaften eines Kreises ab. Pi (π) stellt das Verhältnis des Umfangs eines Kreises zu seinem Durchmesser dar. Multipliziert man den Radius (r) mit 2π, berechnet man im Wesentlichen die Entfernung um den Kreis, die die Definition des Kreisumfangs darstellt.
Beträgt der Umfang das 3.14-fache des Radius?
Nein, der Umfang ist nicht genau 3.14 mal Radius. Die Beziehung zwischen Umfang und Radius eines Kreises ergibt sich aus der Formel C = 2πr. Während π (Pi) ungefähr 3.14159 beträgt, beträgt der Umfang 2 mal π mal Radius. Der Umfang ist also mehr als nur 3.14 mal Radius; er ist 2 mal π mal Radius.
Ref: Omni-Rechner | Proprof
