Jak dokładnie obliczyć obwód koła?
Obwód koła to podstawowa i wymagana wiedza matematyczna wprowadzana w szkole podstawowej lub średniej. Opanowanie obwodu koła jest niezbędne dla uczniów, którzy planują kontynuować bardziej zaawansowane kursy matematyki w szkole średniej i na studiach oraz przygotować się do egzaminów standaryzowanych, takich jak SAT i ACT.
Quiz „Obwód koła” w tym artykule ma na celu sprawdzenie Twojej wiedzy na temat znajdowania promienia, średnicy i obwodu koła.
Spis treści:
Wzór na obwód koła
Zanim przejdziemy do testu, podsumujmy kilka najważniejszych informacji!
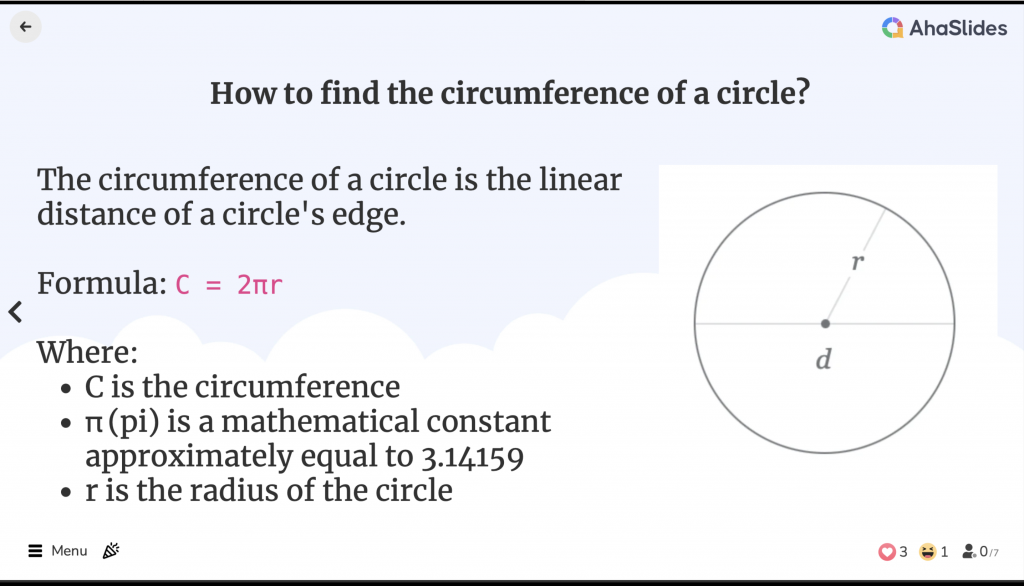
Jaki jest obwód koła?
Obwód okręgu to liniowa odległość krawędzi okręgu. Jest to równoważne obwodowi kształtu geometrycznego, chociaż termin obwód jest używany tylko w odniesieniu do wielokątów.
Jak znaleźć obwód koła?
Wzór na obwód koła jest następujący:
C = 2πr
gdzie:
- C to obwód
- π (pi) to stała matematyczna równa w przybliżeniu 3.14159
- r jest promieniem okręgu
Promień to odległość od środka okręgu do dowolnego punktu na krawędzi.
Średnica jest dwa razy większa od promienia, więc obwód można również wyrazić jako:
C = πd
gdzie:
- d to średnica
Na przykład, jeśli promień okręgu wynosi 5 cm, to obwód wynosi:
C = 2πr = 2π * 5 cm = 10π cm
≈ 31.4 cm (zaokrąglone do 2 miejsc po przecinku)
Więcej wskazówek od AhaSlides
- Ponad 70 pytań do quizu matematycznego do zabawnych ćwiczeń w klasie
- 10 najlepszych gier matematycznych w klasie dla znudzonych uczniów K12
- 60 niesamowitych pomysłów na łamigłówki dla dorosłych | Aktualizacje 2023
AhaSlides to najlepszy kreator quizów
Twórz interaktywne gry w mgnieniu oka, korzystając z naszej obszernej biblioteki szablonów, która zabije nudę

Quiz na temat obwodu koła
Pytanie 1: Jeśli obwód okrągłego basenu wynosi 50 metrów, jaki jest jego promień?
A. 7.95 metra
B. 8.00 metrów
C. 15.91 metrów
D.25 metrów
✅ Poprawna odpowiedź:
A. 7.95 metra
Wyjaśnienie:
Promień można znaleźć, przekształcając wzór C = 2πr i rozwiązując dla r: r = C / (2π). Podstawiając podany obwód 50 metrów i przybliżając π do 3.14, otrzymujemy promień wynoszący około 7.95 metra.
Pytanie 2: Średnica okręgu wynosi 14 cali. Jaki jest jego promień?
A. 28 cali
B.14 cali
C. 21 cali
D. 7 cali
✅ Poprawna odpowiedź:
D. 7 cali
Wyjaśnienie:
Ponieważ średnica jest dwa razy większa od długości promienia (d = 2r), możesz obliczyć promień, dzieląc średnicę przez 2 (r = d / 2). W tym przypadku podzielenie danej średnicy 14 cali przez 2 daje promień 7 cali.

Pytanie 3: Które z poniższych stwierdzeń jest prawdziwe w odniesieniu do związku między średnicą a obwodem koła?
A. Średnica stanowi połowę obwodu.
B. Średnica jest taka sama jak obwód.
C. Średnica jest dwa razy większa od obwodu.
D. Średnica jest π razy większa od obwodu.
✅ Poprawna odpowiedź:
A. Średnica stanowi połowę obwodu.
Wyjaśnienie:
Średnica jest równa 2-krotności promienia, a obwód jest równy 2π-krotności promienia. Zatem średnica jest połową obwodu.
Pytanie 4: Stół, przy którym mamy usiąść, ma obwód 6.28 jarda. Musimy znaleźć średnicę stołu.
A. 1 jard
B. 2 jardy
C. 3 jardy
D. 4 jardy
✅ Poprawna odpowiedź:
B. 2 jardy
Wyjaśnienie:
Obwód koła oblicza się, mnożąc średnicę przez pi (π). W tym przypadku obwód wynosi 6.28 jarda. Aby znaleźć średnicę, musimy podzielić obwód przez pi. Dzieląc 6.28 jarda przez pi, otrzymujemy około 2 jardy. Zatem średnica stołu wynosi 2 jardy.
Pytanie 5: Okrągły ogród ma obwód 36 metrów. Jaki jest przybliżony promień ogrodu?
A. 3.14 metra
B. 6 metrów
C. 9 metrów
D.18 metrów
✅ Poprawna odpowiedź:
C. 9 metrów
Wyjaśnienie:
Aby znaleźć promień, użyj wzoru na obwód: C = 2πr. Przekształć wzór, aby obliczyć promień: r = C / (2π). Podstawiając podany obwód 36 metrów i używając przybliżonej wartości π jako 3.14, otrzymujesz r = 36 / (2 * 3.14) ≈ 9 metrów.
Pytanie 6: Okrągły basen ma promień 8 metrów. Jaki jest przybliżony dystans, jaki pokonuje pływak wokół basenu, kończąc jedno okrążenie?
A. 16 metra
B. 25 metrów
C. 50 metrów
D.100 metrów
✅ Poprawna odpowiedź:
C. 50 metrów
Wyjaśnienie:
Aby obliczyć odległość, jaką pływak pokonuje wokół basenu podczas jednego okrążenia, należy użyć wzoru na obwód (C = 2πr). W tym przypadku jest to 2 * 3.14 * 8 metrów ≈ 50.24 metra, co daje w przybliżeniu 50 metrów.
Pytanie 7: Podczas pomiaru hula hop w klasie grupa C odkryła, że ma promień 7 cali. Jaki jest obwód hula hop?
A. 39.6 cali
B. 37.6 cala
C. 47.6 cali
D. 49.6 cali
✅ Poprawna odpowiedź:
C. 47.6 cali
Wyjaśnienie:
Obwód koła można obliczyć, korzystając ze wzoru C = 2πr, gdzie r jest promieniem koła. W tym przypadku promień hula hoop wynosi 7 cali. Podstawiając tę wartość do wzoru, otrzymujemy C = 2π(7) = 14π cali. Przybliżając π do 3.14, możemy obliczyć obwód jako 14(3.14) = 43.96 cala. Zaokrąglony do najbliższej dziesiątej, obwód wynosi 47.6 cala, co odpowiada podanej odpowiedzi.
Pytanie 8: Półkole ma promień 10 metrów. Jaki jest jego obwód?
A. 20 metra
B. 15 metrów
C. 31.42 metrów
D.62.84 metrów
✅ Poprawna odpowiedź:
C. 31.42 metrów
Wyjaśnienie: Aby obliczyć obwód półkola, należy obliczyć połowę obwodu pełnego koła o promieniu 10 metrów.

Pytanie 9: Drużyna koszykówki gra piłką o promieniu 5.6 cala. Jaki jest obwód każdej piłki do koszykówki?
A. 11.2 cali
B. 17.6 cala
C. 22.4 cali
D. 35.2 cali
✅ Poprawna odpowiedź:
C. 22.4 cali
Wyjaśnienie:
Możesz użyć wzoru na obwód koła, który wynosi C = 2πr. Podany promień wynosi 5.6 cala. Podstaw tę wartość do wzoru, mamy C = 2π * 5.6 cala. C ≈ 2 * 3.14 * 5.6 cala. C ≈ 11.2 * 5.6 cala. C ≈ 22.4 cala. Tak więc obwód każdej piłki do koszykówki wynosi około 22.4 cala. Reprezentuje to odległość wokół piłki do koszykówki.
Pytanie 10: Sarah i jej dwie przyjaciółki budowały okrągły stół piknikowy na swoje spotkanie. Wiedzieli, że aby wszyscy mogli wygodnie usiąść przy stole, potrzebny jest obwód 18 stóp. Jaką średnicę musi mieć stół piknikowy, aby osiągnąć prawidłowy obwód?
A. 3 stopy
B. 6 stóp
C. 9 stóp
D. 12 stóp
✅ Poprawna odpowiedź:
B. 6 stóp
Wyjaśnienie:
Aby obliczyć promień, podziel obwód przez 2π. Mamy r = C / (2π) r = 18 stóp / (2 * 3.14) r ≈ 18 stóp / 6.28 r ≈ 2.87 stopy (zaokrąglone do najbliższej setnej).
Teraz, aby znaleźć średnicę, po prostu podwój promień: Średnica = 2 * Promień Średnica ≈ 2 * 2.87 stopy Średnica ≈ 5.74 stopy. Tak więc stół piknikowy musi mieć średnicę około 5.74 stopy.
Kluczowe dania na wynos
AhaSlajdy jest najlepszym interaktywnym twórcą quizów, który może być używany do celów edukacyjnych, szkoleniowych lub rozrywkowych. Sprawdź AhaSlides już teraz, aby otrzymać bezpłatne konfigurowalne szablony i zaawansowane funkcje!
Najczęściej zadawane pytania
Ile wynosi 2πr okręgu?
2πr to wzór na obwód koła. W tym wzorze:
- „2” oznacza, że bierzesz dwukrotność długości promienia. Obwód to odległość wokół okręgu, więc musisz obejść okrąg raz i jeszcze raz, dlatego mnożymy przez 2.
- „π” (pi) to stała matematyczna równa w przybliżeniu 3.14159. Jest używana, ponieważ przedstawia zależność między obwodem a średnicą okręgu.
- „r” oznacza promień okręgu, który jest odległością od środka okręgu do dowolnego punktu na jego obwodzie.
Dlaczego obwód wynosi 2πr?
Wzór na obwód okręgu, C = 2πr, pochodzi z definicji pi (π) i geometrycznych właściwości okręgu. Pi (π) reprezentuje stosunek obwodu okręgu do jego średnicy. Kiedy mnożysz promień (r) przez 2π, zasadniczo obliczasz odległość wokół okręgu, co jest definicją obwodu.
Czy obwód jest 3.14 razy większy od promienia?
Nie, obwód nie jest dokładnie 3.14 razy większy od promienia. Związek między obwodem a promieniem okręgu jest podany wzorem C = 2πr. Podczas gdy π (pi) wynosi w przybliżeniu 3.14159, obwód jest 2 razy π razy większy od promienia. Tak więc obwód jest większy niż 3.14 razy większy od promienia; jest 2 razy π razy większy od promienia.
Ref: Kalkulator Omni | prof